山东省济宁市曲阜市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 要使二次根式 有意义, 的值可以是( )A、 B、 C、 D、2. 一次函数 与x轴的交点为( )A、(1,1) B、(0,2) C、(2,0) D、(3,0)3. 在▱ABCD中,如果 ,那么 的度数是( )A、115º B、65º C、25º D、35º4. 某青年排球队12名队员的年龄情况如下表所示:
年龄
18
19
20
21
22
人数
1
4
3
2
2
则这12名队员的平均年龄是( )
A、18岁 B、19岁 C、20岁 D、21岁5. 以下列各组数为边长,能构成直角三角形的是( )A、5,12,13 B、1,2, C、 , ,2 D、4,5,66. 下列运算结果正确的是( )A、 =﹣3 B、(﹣ )2=2 C、 ÷ =2 D、 =±47. 已知四边形ABCD是平行四边形,下列结论错误的是( )A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当 时,它是矩形 D、当 时,它是菱形8. 某校举行“汉字听写比赛”,5个班级代表队的符合题意答题数如图.这5个符合题意答题数所组成的一组数据的中位数和众数分别是( ) A、10,15 B、13,15 C、13,20 D、15,159. 在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )
A、10,15 B、13,15 C、13,20 D、15,159. 在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )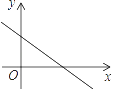 A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<010. 已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )
A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<010. 已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )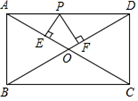 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 正比例函数图象经过 ,则这个正比例函数的解析式是.12. 已知: , ,代数式 的值为.13. 已知,如图,一小船以20海里/时的速度从港口A出发向东北方向航行,另一小船以15海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距.
 14. 将直线y=2x-5向上平移2个单位,所得直线解析式为 .15. 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AB边中点,菱形ABCD的周长为24,则OH的长等于 .
14. 将直线y=2x-5向上平移2个单位,所得直线解析式为 .15. 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AB边中点,菱形ABCD的周长为24,则OH的长等于 .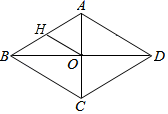 16. 如图,正方形 的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且 ,则四边形 的面积为 .
16. 如图,正方形 的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且 ,则四边形 的面积为 .
三、解答题
-
17. 计算: .18. 如图,每个小正方形的边长都为1.
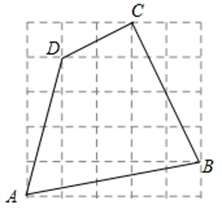 (1)、求四边形ABCD的周长;(2)、求 的度数.19. 甲、乙两名同学5次数学练习(满分150分)的成绩如下表:(单位:分)
(1)、求四边形ABCD的周长;(2)、求 的度数.19. 甲、乙两名同学5次数学练习(满分150分)的成绩如下表:(单位:分)测试日期
2月10日
2月20日
3月5日
3月18日
3月27日
甲
126
127
130
133
134
乙
130
125
130
135
130
已知甲同学这5次数学练习成绩的平均数为130分,方差为10分.
(1)、乙同学这5次数学练习成绩的平均数为分,方差为分;(2)、甲、乙都认为自己在这5次练习中的表现比对方更出色,请分别写出一条支持他们俩观点的理由.20. 如图,在平行四边形ABCD中,E、F为对角线BD上的两点,且∠BAF=∠DCE.求证:BE=DF.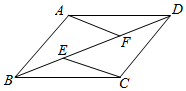 21. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
21. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1. (1)、求k,b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集;(3)、M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.22. “双剑合璧,天下无敌”,其意思是指两个人合在一起,取长补短,威力无比.在二次根式中也常有这种相辅相成的“对子”,如: , ,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解: , .
(1)、求k,b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集;(3)、M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.22. “双剑合璧,天下无敌”,其意思是指两个人合在一起,取长补短,威力无比.在二次根式中也常有这种相辅相成的“对子”,如: , ,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解: , .像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.
解决下列问题:
(1)、将 分母有理化得; 的有理化因式是;(2)、化简: =;(3)、化简: ……+ .23. 如图,矩形 中,点 是线段 上一动点, 为 的中点, 的延长线交BC于 . (1)、求证: ;(2)、若 , , 从点 出发,以l 的速度向 运动(不与 重合).设点 运动时间为 ,请用 表示 的长;并求 为何值时,四边形 是菱形.
(1)、求证: ;(2)、若 , , 从点 出发,以l 的速度向 运动(不与 重合).设点 运动时间为 ,请用 表示 的长;并求 为何值时,四边形 是菱形.