山东省济南市天桥区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-17 类型：期末考试

进入出卷网下载

一、单选题

1. 若m＞n，则下列不等式中不成立的是（）

A、m＋3＞n＋3 B、－2m＞－2n C、m－2＞n－2 D、 $\frac{m}{3} > \frac{n}{3}$

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列等式从左到右的变形是因式分解的是（）

A、 $12 a^{2} b = 3 a \cdot 4 a b$ B、 $(x + 3) (x - 3) = x^{2} - 9$ C、 $a x - a y = a (x - y)$ D、 $4 x^{2} + 8 x - 1 = 4 x (x + 2) - 1$

查看试题解析
4. 计算 $\frac{a - 1}{a} + \frac{1}{a}$ ，正确的结果是（）

A、1 B、 $\frac{1}{2}$ C、 a D、 $\frac{1}{a}$

查看试题解析
5. 在平面直角坐标系中，将点A（1，－2）向左平移2个单位长度，再向上平移3个单位长度，得到点A′，则点A的坐标是（）

A、（－1，1） B、（－1，－2） C、（－1，2） D、（1，2）

查看试题解析
6. 一个不等式组的解集在数轴上的表示如下图，则这个不等式组的解集是（）

A、x<3 B、x≥－1 C、－1<x≤3 D、－1≤x<3

查看试题解析
7. 如图，在平行四边形ABCD中，AC与BD交于O点，则下列结论中不一定成立的是（）

A、AB＝CD B、AO＝CO C、AC＝BD D、AD∥BC

查看试题解析
8. 一元二次方程2x²-x+1=0的根的情况是（）

A、两个不相等的实数根 B、两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
9. 如图，把 $R t △ A B C$ 绕点A逆时针旋转40°，得到 $R t △ A B^{'} C^{'}$ ，点 $C^{'}$ 恰好落在边AB上，连接 $B B^{'}$ ，则 $∠ B B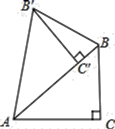^{'} C^{'}$ 的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
10. 如图，直线y＝kx＋b（k≠0）经过点（－1，3），则不等式kx＋b≥3解集为（）

A、x≤－1 B、x≥－1 C、x≤3 D、x≥3

查看试题解析
11.
如图，P是矩形ABCD的对角线AC的中点，E是AD的中点．若AB=6，AD=8，则四边形ABPE的周长为（　　）

A、14 B、16 C、17 D、18

查看试题解析
12. 已知有理数a≠1，我们把 $\frac{1}{1 - a}$ 称为a的差倒数，如：2的差倒数是 $\frac{1}{1 - 2}$ ＝－1，－1的差倒数 $\frac{1}{1 - (- 1)}$ ＝ $\frac{1}{2}$ ．如果a₁＝－2，a₂是a₁的差倒数，a₃是a₂的差倒数，a₄是a₃的差倒数……依此类推，那么a₁＋a₂＋……＋a₁₀₀的值是（）

A、7.35 B、－7.5 C、5.5 D、－5.5

查看试题解析

二、填空题

13. 分解因式：ab﹣b²= ．

查看试题解析
14. 一个多边形的每一个外角都是36°，则这个多边形的边数是．

查看试题解析
15. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x= ．

查看试题解析
16. 如图，在 $▱ A B C D$ 中，将 $Δ A D C$ 沿 $A C$ 折叠后，点 $D$ 恰好落在 $D C$ 的延长线上的点 $E$ 处．若 $∠ B = 60 °$ ， $A B = 3$ ，则 $Δ A D E$ 的周长为．

查看试题解析
17. 将矩形纸片ABCD按如图所示的方式折叠，恰好得到菱形AECF．若AB＝3，则菱形AECF的面积为．

查看试题解析
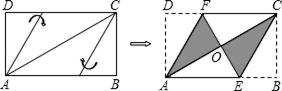18. 如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与点B，C重合），过点C作CN⊥DM交AB于点N，连结OM、ON，MN．下列五个结论：①△CNB≌△DMC；②ON＝OM；③ON⊥OM；④若AB＝2，则S_△_OMN的最小值是1；⑤AN²+CM²＝MN² ．其中正确结论是；（只填序号）

查看试题解析

三、解答题

19. 解不等式组： ${\begin{array}{l} 2 x - 1 < x - 3 \\ \frac{x + 1}{2} > x - 1 \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
20. 先化简，再求值：（ $\frac{x^{2}}{x - 1}$ ＋ $\frac{1}{1 - x}$ ）÷ $\frac{x + 1}{x - 1}$ ，其中x＝2020．

查看试题解析
21. 如图，▱ABCD的对角线AC，BD相交于点O，点E、F在BD上，且BE＝DF，求证：四边形AECF是平行四边形.

查看试题解析
22.

(1)、分解因式：2x³－8x；

(2)、解方程：x²－2x－1＝0

查看试题解析
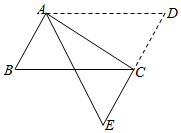
23. $△$ ABC在平面直角坐标系xOy中的位置如图所示． A （－2，3）， B（－1，1）， C（0，2）

(1)、将 $△$ ABC向右平移2个单位，作出平移后的 $△$ A₁B₁C₁；

(2)、作出 $△$ A₁B₁C₁关于点C₁成中心对称的图形 $△$ A₂B₂C₂；

(3)、连接A₂B₁ ，则 $△$ A₂B₂B₁的面积为．

查看试题解析
24. 复课返校后，为了拉大学生锻炼的间距，某学校决定增购适合独立训练的两种体育器材：跳绳和毽子．已知跳绳的单价比毽子的单价多5元，用400元购买的跳绳个数和用150元购买的毽子个数相同．

(1)、求跳绳和毽子的单价分别是多少元？

(2)、学校准备一次性购买跳绳和毽子两种器材共120个，但总费用不超过600元，那么最多可购买多少根跳绳？

查看试题解析
25. 已知：如图，平行四边形ABCD中，E是BC的延长线上一点，CE＝CB，AE交CD 于点O．

(1)、求证：OC＝OD；

(2)、连接AC、DE，当∠B＝∠AEB时，判断四边形ACED的形状，并说明理由；

(3)、在（2）条件下，∠B＝°时，四边形ACED是正方形．

查看试题解析
26.

(1)、认识模型：如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于D，过B作BE⊥ED于E．求证： $△$ BEC≌ $△$ CDA；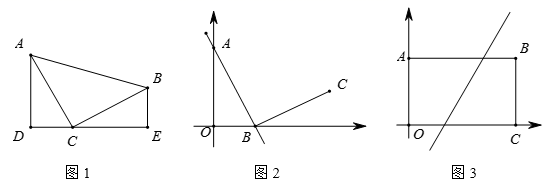

(2)、应用模型：①已知直线y＝－2x＋4与y轴交于A点，与x轴交于B点，将线段AB绕点B顺时针旋转90度，得到线段CB，求点C的坐标；
②如图3，矩形ABCO，O为坐标原点，B的坐标为（5，4），A，C分别在坐标轴上，P是线段BC上动点，已知点D在第一象限，且是直线y＝2x－3上的一点，点Q是平面内任意一点．若四边形ADPQ是正方形，请直接写出所有符合条件的点D的坐标．

查看试题解析
27. 如图1，在等边 $△$ ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动，动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动，设运动时间为t（s）．过点P作PE⊥AC于E，以CQ、CE为边作平行四边形CQFE．

(1)、AE＝， CE＝；（用含t的代数式表示）

(2)、当平行四边形CQFE为菱形时，请求出t的值；

(3)、如图1，连接PQ，交AC边于点D，求线段DE的长；

(4)、如图2，取线段BC的中点M，连接PM，将 $△$ BPM沿直线PM翻折，得 $△ B^{'} P M$ ，连接 $A B^{'}$ ，请求出 $A B^{'}$ 的最小值．

查看试题解析