山东省济南市市中区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 若 ,则下列式子中错误的是( )A、 B、 C、 D、2. 下列图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列从左边到右边的变形,属于因式分解的是( )A、(x+1)(x-1)=x2-1 B、x2-2x+1=x(x-2)+1 C、a(x-y)=ax-ay D、x2+2x+1=(x+1)24. 要使分式 有意义,则 的取值范围是( )A、 B、 C、 D、5. 不等式x-1<0的解集在数轴上表示正确的是( )A、
3. 下列从左边到右边的变形,属于因式分解的是( )A、(x+1)(x-1)=x2-1 B、x2-2x+1=x(x-2)+1 C、a(x-y)=ax-ay D、x2+2x+1=(x+1)24. 要使分式 有意义,则 的取值范围是( )A、 B、 C、 D、5. 不等式x-1<0的解集在数轴上表示正确的是( )A、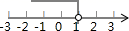 B、
B、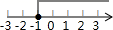 C、
C、 D、
D、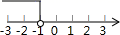 6. 如图,一个长为2、宽为1的长方形以下面的“姿态”从直线 的左侧水平平移至右侧(下图中的虚线是水平线),其中,平移的距离是( )
6. 如图,一个长为2、宽为1的长方形以下面的“姿态”从直线 的左侧水平平移至右侧(下图中的虚线是水平线),其中,平移的距离是( ) A、1 B、2 C、3 D、7. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )
A、1 B、2 C、3 D、7. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )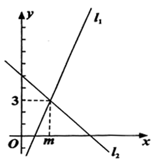 A、 B、 C、 D、8. 下面的多边形中,内角和与外角和相等的是( )A、
A、 B、 C、 D、8. 下面的多边形中,内角和与外角和相等的是( )A、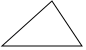 B、
B、 C、
C、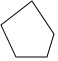 D、
D、 9. 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
9. 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )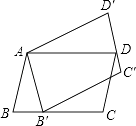 A、100° B、105° C、115° D、120°10. 化简 的结果是( )A、m+3 B、m﹣3 C、 D、11. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点C作CE⊥AD于点E , 连接OE , 若OB=8,S菱形ABCD=96,则OE的长为( )
A、100° B、105° C、115° D、120°10. 化简 的结果是( )A、m+3 B、m﹣3 C、 D、11. 如图,菱形ABCD的对角线AC、BD相交于点O , 过点C作CE⊥AD于点E , 连接OE , 若OB=8,S菱形ABCD=96,则OE的长为( ) A、2 B、2 C、6 D、812. 如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为( )
A、2 B、2 C、6 D、812. 如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为( ) A、0.5 B、2.5 C、 D、1
A、0.5 B、2.5 C、 D、1二、填空题
-
13. 分解因式:x2-2x+1=.14. 当x=时,分式 的值为零.
15. 若关于x的分式方程 = 有增根,则m的值为 .16. 两个实数 , ,规定 ,则不等式 的解集为.17. 如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 . 18. 如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN= .
18. 如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN= .
三、解答题
-
19. 化简:20. 解不等式组: ,并在数轴上表示解集.21. 如图,在□ABCD中,E、F分别是DA、BC延长线上的点,且∠ABE=∠CDF.求证:AE=CF.
 22.(1)、因式分解:2y2-8(2)、解方程:23. 平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).其中A(1,1)、B(4,4)、C(5,1).
22.(1)、因式分解:2y2-8(2)、解方程:23. 平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).其中A(1,1)、B(4,4)、C(5,1). (1)、将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1 .(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△A2B2C2 , A、B、C的对应点分别为A2、B2、C2 .(3)、先化简,再求值: ,其中a=5.24. 某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)、将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1 .(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△A2B2C2 , A、B、C的对应点分别为A2、B2、C2 .(3)、先化简,再求值: ,其中a=5.24. 某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)、求A,B两种型号的机器人每小时分别搬运多少材料;
(2)、该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
25. 如图,点E,F分别在矩形ABCD的边AB,CD上,且∠DAF=∠BCE. (1)、求证:AF=CE;(2)、连接AC,若AC平分∠FAE,∠DAF=30°,CE=4,求CD的长.26. 装饰公司为小明家设计电视背景墙时需要A、B型板材若干块,A型板材规格是a´b,B型板材规格是b´b.现只能购得规格是150´b的标准板材.(单位:cm)(1)、若设a=60cm,b=30cm.一张标准板材尽可能多的裁出A型、B型板材,共有下表三种裁法,下图是裁法一的裁剪示意图.
(1)、求证:AF=CE;(2)、连接AC,若AC平分∠FAE,∠DAF=30°,CE=4,求CD的长.26. 装饰公司为小明家设计电视背景墙时需要A、B型板材若干块,A型板材规格是a´b,B型板材规格是b´b.现只能购得规格是150´b的标准板材.(单位:cm)(1)、若设a=60cm,b=30cm.一张标准板材尽可能多的裁出A型、B型板材,共有下表三种裁法,下图是裁法一的裁剪示意图.裁法一
裁法二
裁法三
A型板材块数
1
2
0
B型板材块数
3
m
n
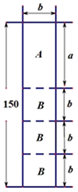
则上表中, m= , n=;
(2)、为了装修的需要,小明家又购买了若干C型板材,其规格是a´a,并做成如下图的背景墙.请写出下图中所表示的等式:; (3)、若给定一个二次三项式2a2+5ab+3b2 , 试用拼图的方式将其因式分解.(请仿照(2)在几何图形中标上有关数量)27. 如图1,E为正方形ABCD的边BC上一点,F为边BA延长线上一点,且CE=AF.
(3)、若给定一个二次三项式2a2+5ab+3b2 , 试用拼图的方式将其因式分解.(请仿照(2)在几何图形中标上有关数量)27. 如图1,E为正方形ABCD的边BC上一点,F为边BA延长线上一点,且CE=AF. (1)、求证:DE⊥DF;(2)、如图2,若点G为边AB上一点,且∠BGE=2∠BFE,△BGE的周长为16,求四边形DEBF的面积;(3)、如图3,在(2)的条件下,DG与EF交于点H,连接CH且CH=5
(1)、求证:DE⊥DF;(2)、如图2,若点G为边AB上一点,且∠BGE=2∠BFE,△BGE的周长为16,求四边形DEBF的面积;(3)、如图3,在(2)的条件下,DG与EF交于点H,连接CH且CH=5 ,求AG的长.
,求AG的长.