山东省济南市平阴县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列从左到右的变形，是分解因式的为（）

A、x²－x=x(x－1) B、a(a－b)=a²－ab C、(a+3)(a－3)=a²－9 D、x²－2x+1=x(x－2)+1

查看试题解析
3. 已知x＞y，那么下列不等式成立的是（）

A、x－6＜y－6 B、3x＜3y C、－2x＜－2y D、－x＞－y

查看试题解析
4. 已知 $\frac{b}{a}$ ＝2，则 $\frac{a - b}{a + b}$ 的值是（）

A、 $\frac{1}{3}$ B、－ $\frac{1}{3}$ C、3 D、－3

查看试题解析
5. 在四边形ABCD中，对角线AC、BD 相交于点O，下列条件中不一定能判定这个四边形是平行四边形的是（）

A、 $A B // D C$ ，AD＝BC B、 $A B // D C$ ， $A D // B C$ C、OA＝OC，OB＝OD D、AB＝DC，AD＝BC

查看试题解析
6. 已知 $\frac{x^{2} - 4}{(x - 2) (x - 1)}$ 的值等于0，则x的大小为（）

A、1 B、2 C、土2 D、－2

查看试题解析
7. 如果不等式组 ${\begin{matrix} x > 4 \\ x > n \end{matrix}$ 的解集是 $x > 4$ ，则n的取值范围是（）

A、n≥4 B、 $n = 4$ C、n≤4 D、 $n < 4$

查看试题解析
8. 如果把分式 $\frac{x}{x - y}$ 中的 $x$ 、 $y$ 的值都扩大为原来的2倍，那么分式的值（）

A、扩大为原来的2倍 B、缩小为原来的一半 C、扩大为原来的4倍 D、保持不变

查看试题解析
9. 如图，一次函数 $y = k x + b$ 的图像经过 $A$ ， $B$ 两点，则 $k x + b > 0$ 解集是（）

A、 $x > 0$ B、 $x > 2$ C、 $x > - 3$ D、 $- 3 < x < 2$

查看试题解析
10. 如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为（）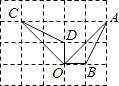

A、30° B、45° C、90° D、135°

查看试题解析
11.
如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（　　）

A、3cm B、6cm C、9cm D、12cm

查看试题解析
12. 如图， $▱ A B C D$ 的对角线AC、BD相较于点O，AE平分∠BAD交BC于点E，∠ADC＝60°，AB＝ $\frac{1}{2}$ BC，连接OE，下列结论：①∠CAD＝30°；② $S_{▱ A B C D} = A B \cdot A C$ ；③OA＝OB；④OE＝ $\frac{1}{4}$ BC．其中成立的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 分解因式：2x²﹣8=

查看试题解析
14. 已知方程组 ${\begin{array}{l} 2 x + y = 2 + 4 m \\ x + 2 y = 1 - m \end{array}$ 的解满足x＋y＜0，则m的取值范围是；

查看试题解析
15. 若关于x的方程 $\frac{x - 8 + k}{x - 7} = 8$ 有增根，则k的值是．

查看试题解析
16. 如图所示，将矩形ABCD对折，设折痕为MN，再把B点叠在折痕MN上（如图点B′），若AB＝ $\sqrt{3}$ ，则折痕AE的长为；

查看试题解析
17. 菱形OBCD在平面直角坐标系中的位置如图所示，顶点B（2 $\sqrt{3}$ ，0），∠DOB＝60°，点P是对角线OC上一个动点，E（0，－1），则EP十BP的最小值为．

查看试题解析

三、解答题

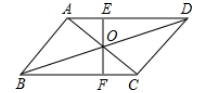
18. 因式分解：

(1)、2x²－4xy＋2y²；

(2)、x⁴－16

查看试题解析
19. 解分式方程： $\frac{2 - x}{x - 3}$ ＝1＋ $\frac{1}{3 - x}$

查看试题解析
20. 先化简 $\frac{x^{2} - 4}{x^{2} - 9}$ ÷（1＋ $\frac{1}{x - 3}$ ），并求x＝1时代数式的值．

查看试题解析
21. 已知：如图， $▱ A B C D$ 的对角线AC与BD相交于点O，过点O的直线与AD、CB分别相交于点E、F．求证：OE＝OF．

查看试题解析
22. 某内陆城市为了落实国家“一带一路”倡议，促进经济发展，增强对外贸易的竞争力，把距离港口420km的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2h，求汽车原来的平均速度．

查看试题解析
23. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立直角坐标系中， $△ A B C$ 的顶点均在格点上，点C（4，－1）．

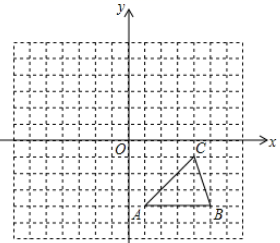(1)、把 $△ A B C$ 向上平移5个单位长度后得到对应的 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并写出C₁的坐标；

(2)、以原点O为对称中心，再画出 $△ A B C$ 关于原点O对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点C₂的坐标；

(3)、请直接写出 $▱ A B C D$ 的第四个顶点D的坐标．

查看试题解析
24. 王老师安排喜欢探究问题的小明同学解决某个问题前，先让小明看了一个有解答过程的例题．
例：若m²＋2mn＋2n²－6n＋9＝0，求m和n的值．

解：∵m²＋2mn＋2n²－6n＋9＝0，

∴m²＋2mn＋n²＋n²－6n＋9＝0．

即：（m＋n）²＋（n－3）²＝0，

∴m＋n＝0，n－3＝0，

∴m＝－3，n＝3．

为什么要对2n²进行了拆项呢？聪明的小明理解了例题解决问题的方法，很快解决了下面两个问题．相信你也能很好的解决下面的这两个问题，请写出你的解题过程．

(1)、若x²－4xy＋5y² ＋2y＋1＝0，求x^y的值；

(2)、已知a、b、c是等腰△ABC的三边长，且满足a²－10a＋b²－12b＋61＝0，求此三角形的周长．

查看试题解析
25.

(1)、如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°．

①当点D在AC上时，如图1，线段BD、CE有怎样的数量关系和位置关系？直接写出你猜想的结论；

②将图1中的△ADE绕点A顺时针旋转α角（0°＜α＜90°），如图2，线段BD、CE有怎样的数量关系和位置关系？请说明理由．

(2)、当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时，使线段BD、CE在（1）中的位置关系仍然成立？不必说明理由．
甲：AB：AC=AD：AE=1，∠BAC=∠DAE≠90°；

乙：AB：AC=AD：AE≠1，∠BAC=∠DAE=90°；

丙：AB：AC=AD：AE≠1，∠BAC=∠DAE≠90°．

查看试题解析
26. 如图1，在矩形纸片ABCD中，AB＝3cm，AD＝5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．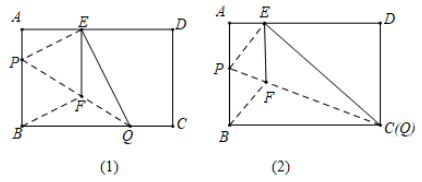

(1)、求证：四边形BFEP为菱形；

(2)、当E在AD边上移动时，折痕的端点P、Q也随着移动．
①当点Q与点C重合时，（如图2），求菱形BFEP的边长；

②如果限定P、Q分别在线段BA、BC上移动，直接写出菱形BFEP面积的变化范围．

查看试题解析