山东济南南山区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 下列等式从左到右的变形,属于因式分解的是( )A、a(x-y)=ax-ay B、a2-b2=(a+b)( a-b) C、x2+2x+1=x(x+2)+1 D、(x+1)( x+3)=x2+4x+32. 已知x>y,则下列不等式成立的是( )A、﹣2x>﹣2y B、3x>3y C、6﹣x>6﹣y D、﹣3. 要使分式 有意义,则x的取值应满足( )A、x≠4 B、x≠﹣1 C、x=4 D、x=﹣14. 在 中,∠A∶∠B∶∠C∶∠D可能是( )A、1∶2∶2∶1 B、1∶2∶3∶4 C、2∶1∶1∶2 D、2∶1∶2∶15. 不等式3x+3≤0的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、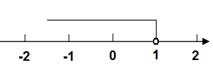 D、
D、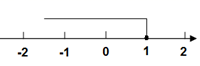 6. 计算 的结果为( )A、﹣1 B、1 C、 D、7. 矩形ABCD中,对角线AC、BD交于点O,如果AB=4,∠AOB=60°,那么AC的长等于( )A、16 B、8 C、16 D、88. 如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
6. 计算 的结果为( )A、﹣1 B、1 C、 D、7. 矩形ABCD中,对角线AC、BD交于点O,如果AB=4,∠AOB=60°,那么AC的长等于( )A、16 B、8 C、16 D、88. 如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )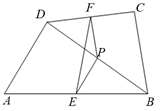 A、50° B、40° C、30° D、20°9. 在一个不透明的盒子里装有若干个白球和15个红球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到红球的频率稳定在0.6左右,则袋中白球约有( )A、10个 B、12个 C、15个 D、25个10. 若n边形的内角和等于外角和的3倍,则边数n为( )A、n=6 B、n=7 C、n=8 D、n=911. 如图,一次函数y1=x+b与一次函数y2=kx+3的图象交于点P(1,2),则关于不等式x+b kx+3的解集是( )
A、50° B、40° C、30° D、20°9. 在一个不透明的盒子里装有若干个白球和15个红球,这些球除颜色不同外其余均相同,每次从袋子中摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到红球的频率稳定在0.6左右,则袋中白球约有( )A、10个 B、12个 C、15个 D、25个10. 若n边形的内角和等于外角和的3倍,则边数n为( )A、n=6 B、n=7 C、n=8 D、n=911. 如图,一次函数y1=x+b与一次函数y2=kx+3的图象交于点P(1,2),则关于不等式x+b kx+3的解集是( ) A、x 0 B、x 0 C、x 1 D、x 112. 如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为( )
A、x 0 B、x 0 C、x 1 D、x 112. 如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为( ) A、2 B、4 C、 D、
A、2 B、4 C、 D、二、填空题
-
13. 分解因式:a2-4=.14. 已知关于x的方程x2+kx-2=0的一个根是x=2,则另外一个根为 .15. 如图,E为▱ABCD的边AD上任意一点,▱ABCD的面积为6,则图中阴影部分的面积为 .
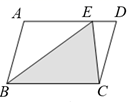 16. 如图所示,直线y=kx+b经过点(﹣2,0),则关于x的不等式kx+b<0的解集为 .
16. 如图所示,直线y=kx+b经过点(﹣2,0),则关于x的不等式kx+b<0的解集为 .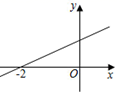 17. 如图,在菱形ABCD中,点E是AB上的一点,连结DE交AC于点O,连结BO,且∠AED=50°,则∠CBO=度.
17. 如图,在菱形ABCD中,点E是AB上的一点,连结DE交AC于点O,连结BO,且∠AED=50°,则∠CBO=度. 18. 如图,E、F分别是正方形ABCD的边AD、BC上的两个定点,M是线段EF上的一点,过M作直线与正方形ABCD的边交于点P和点H,且PH=EF,则满足条件的直线PH最多有条.
18. 如图,E、F分别是正方形ABCD的边AD、BC上的两个定点,M是线段EF上的一点,过M作直线与正方形ABCD的边交于点P和点H,且PH=EF,则满足条件的直线PH最多有条.
三、解答题
-
19.(1)、分解因式:3x2-6x+3(2)、解不等式组20. 解方程: .21. 如图,▱ABCD中,点E、F是对角线AC上的两点,且AE=CF.
求证:BF DE.
 22. 今年突发新冠疫情,某口罩厂接到生产10万只一次性口罩的订单,全体职工加班加点,实际每天生产的数量是平时的2倍,结果比平时提前5天完成任务.求该厂平时每天生产口罩多少万只?23. 如图,幼儿园某教室矩形地面的长为8m,宽为5m,现准备在地面正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度是多少米?
22. 今年突发新冠疫情,某口罩厂接到生产10万只一次性口罩的订单,全体职工加班加点,实际每天生产的数量是平时的2倍,结果比平时提前5天完成任务.求该厂平时每天生产口罩多少万只?23. 如图,幼儿园某教室矩形地面的长为8m,宽为5m,现准备在地面正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度是多少米? 24. 甲、乙两所医院分别有一男一女共4名医护人员支援武汉抗击疫情.(1)、若从这4名医护人员中随机选1名,则选中的是男医护人员的概率是 .(答案直接填写在答题卡的横线上)(2)、若从支援的4名医护人员中随机选2名,求出这两名医护人员来自不同医院的概率.25. 如图1,在菱形ABCD中,AC=2,BD=2 ,AC,BD相交于点O.
24. 甲、乙两所医院分别有一男一女共4名医护人员支援武汉抗击疫情.(1)、若从这4名医护人员中随机选1名,则选中的是男医护人员的概率是 .(答案直接填写在答题卡的横线上)(2)、若从支援的4名医护人员中随机选2名,求出这两名医护人员来自不同医院的概率.25. 如图1,在菱形ABCD中,AC=2,BD=2 ,AC,BD相交于点O.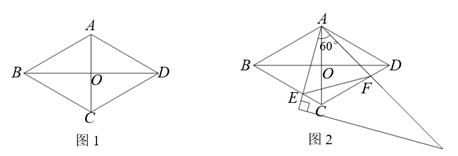 (1)、求边AB的长;(2)、求∠BAC的度数;(3)、如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF.判断△AEF是哪一种特殊三角形,并说明理由.26. (阅读材料)
(1)、求边AB的长;(2)、求∠BAC的度数;(3)、如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF.判断△AEF是哪一种特殊三角形,并说明理由.26. (阅读材料)把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在代数式求值、解方程、最值问题中都有着广泛的应用.
例如:①用配方法因式分解:a2+6a+8.
原式=a2+6a+9-1=(a+3) 2-1=(a+3-1)( a+3+1)=(a+2)(a+4)
②求x2+6x+11的最小值.
解:x2+6x+11=x2+6x+9+2=(x+3) 2+2;
由于(x+3) 2≥0,
所以(x+3) 2+2≥2,
即x2+6x+11的最小值为2.
请根据上述材料解决下列问题:
(1)、在横线上添上一个常数项使之成为完全平方式:a2+4a+;(2)、用配方法因式分解:a2-12a+35;(3)、用配方法因式分解:x4+4;(4)、求4x2+4x+3的最小值.27. 如图,在正方形ABCD中,点E在对角线AC上,点F在射线BC上,且四边形DEFG是正方形,连接CG.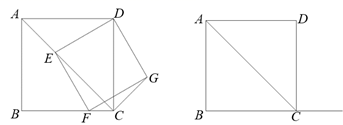 (1)、求证:AE=CG.(2)、求证:∠ACG=90°.(3)、若AB= ,当点E在AC上移动时,AE2+CE2是否有最小值?若有最小值,求出最小值.(4)、当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
(1)、求证:AE=CG.(2)、求证:∠ACG=90°.(3)、若AB= ,当点E在AC上移动时,AE2+CE2是否有最小值?若有最小值,求出最小值.(4)、当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.