江西省新余市2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-17 类型：期末考试

进入出卷网下载

一、单选题

1. 在端午节道来之前，双十中学高中部食堂推荐了A，B，C三家粽子专卖店，对全校师生爱吃哪家店的粽子作调查，以决定最终向哪家店采购．下面的统计量中最值得关注的是（）

A、方差 B、平均数 C、中位数 D、众数

查看试题解析
2. 已知一次函数 $y = k x + b$ 的图象经过一、二、四象限，则下列判断中正确的是（）

A、 $k > 0$ ， $b > 0$ B、 $k < 0$ ， $b > 0$ C、 $k > 0$ ， $b < 0$ D、 $k < 0$ ， $b < 0$

查看试题解析
3. 如图，平行四边形ABCD的对角线AC与BD相交于点O ， AE⊥BC于E ， AB＝ $\sqrt{3}$ ，AC＝2，BD＝4，则AE的长为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{3}{2}$ C、 $\frac{\sqrt{21}}{7}$ D、 $\frac{2 \sqrt{21}}{7}$

查看试题解析
4. 如图，在任意四边形 $A B C D$ 中， $E$ ， $F$ ， $G$ ， $H$ 分别是 $A B$ ， $B C$ ， $C D$ ， $D A$ 上的点，对于四边形 $E F G H$ 的形状，某班学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（）

A、当 $E$ ， $F$ ， $G$ ， $H$ 是各边中点，且 $A C = B D$ 时，四边形 $E F G H$ 为菱形 B、当 $E$ ， $F$ ， $G$ ， $H$ 是各边中点，且 $A C ⊥ B D$ 时，四边形 $E F G H$ 为矩形 C、当 $E$ ， $F$ ， $G$ ， $H$ 不是各边中点时，四边形 $E F G H$ 可以为平行四边形 D、当 $E$ ， $F$ ， $G$ ， $H$ 不是各边中点时，四边形 $E F G H$ 不可能为菱形

查看试题解析

二、填空题

5. 若 $\sqrt{2 x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
6. 如图，在 $▱ A B C D$ 中，已知 $A D = 8 c m$ ， $A B = 6 c m$ ， $D E$ 平分 $∠ A D C$ ，交 $B C$ 边于点E，则 $B E =$ $c m$ ．

查看试题解析
7. 如图由于台风的影响，一棵树在离地面 $6 m$ 处折断，树顶落在离树干底部 $8 m$ 处，则这棵树在折断前的高度是.

查看试题解析
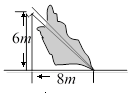8. 我们规定：当k，b为常数，k≠0，b≠0，k≠b时，一次函数y=kx+b与y=bx+k互为交换函数．例如：y=4x+3的交换函数为y=3x+4．一次函数y=kx+2与它的交换函数图象的交点横坐标为．

查看试题解析

三、解答题

9. 如图是一块地的平面图，AD=4m，CD=3m，AB=13m，BC=12m，∠ADC=90°，求这块地的面积.

查看试题解析
10. 图①、图②、图③都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点．线段AB的端点在格点上．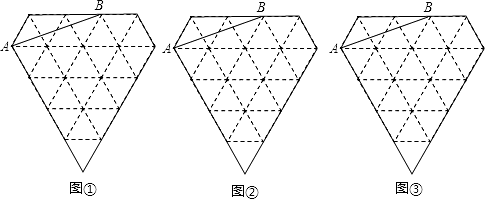

(1)、在图①、图2中，以AB为边各画一个等腰三角形，且第三个顶点在格点上；（所画图形不全等）

(2)、在图③中，以AB为边画一个平行四边形，且另外两个顶点在格点上．

查看试题解析
11. 已知x= $\sqrt{3} - \sqrt{2}$ ,y= $\sqrt{3} + \sqrt{2}$ .

(1)、x+y= ， xy=；

(2)、求x³y+xy³的值.

查看试题解析

12. 八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表(单位：分)：

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9

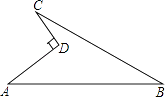
(1)、甲队成绩的中位数是分，乙队成绩的众数是分；

(2)、计算乙队的平均成绩和方差；

(3)、已知甲队成绩的方差是1.4 分 ² ，则成绩较为整齐的是队．

查看试题解析

13. 已知：如图，在菱形 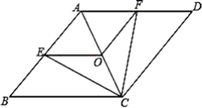$A B C D$ 中，点 $E$ ， $O$ ， $F$ 分别为 $A B$ ， $A C$ ， $A D$ 的中点，连接 $C E$ ， $C F$ ， $O E$ ， $O F$ ．

(1)、求证： $Δ B C E ≌ Δ D C F$ ；

(2)、当 $A B$ 与 $B C$ 满足什么关系时，四边形 $A E O F$ 是正方形？请说明理由．

查看试题解析
14. 某学校计划组织全校1441名师生到相关部门规划的林区植树，经过研究，决定租用当地租车公司62辆A，B两种型号客车作为交通工具．下表是租车公司提供给学校有关两种型号客车的载客量和租金信息：

型号

载客量

租金单价

A

30人/辆

380元/辆

B

20人/辆

280元/辆

注：载客量指的是每辆客车最多可载该校师生的人数．

(1)、设租用A型号客车x辆，租车总费用为y元，求y与x的函数表达式，并写出x的取值范围；

(2)、若要使租车总费用不超过21940元，一共有几种租车方案？哪种租车方案最省钱？

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $E$ 是 $B C$ 的中点，连接 $A E$ ，过点 $B$ 作射线 $B M$ 交 $C D$ 于点 $F$ ，交 $A E$ 于点 $O$ ，且 $B F ⊥ A E$ ．

(1)、求证： $B F = A E$ ；

(2)、连接 $O D$ ，猜想 $O D$ 与 $A B$ 的数量关系，并证明．

查看试题解析
16. 如图，直线 $y = - 2 x + b$ 分别与 $x$ 轴、 $y$ 轴交于 $A$ 、 $B$ 两点，与直线 $y = k x$ 交于点 $C (2 ， 4)$ ，平行于 $y$ 轴的直线 $l$ 从原点 $O$ 出发，以每秒1个单位长度的速度沿 $x$ 轴向右平移，直线 $l$ 分别交直线 $A B$ 、直线 $O C$ 于点 $D$ 、 $E$ ，以 $D E$ 为边向左侧作正方形 $D E F G$ ，当直线 $l$ 经过点 $A$ 时停止运动，设直线 $l$ 的运动时间为 $t$ （秒）．

(1)、 $b =$ ， $k =$ ；

(2)、设线段 $D E$ 的长度为 $d$ （ $d > 0$ ）；求 $d$ 与 $t$ 之间的函数关系式；

(3)、当正方形 $D E F G$ 的边 $G F$ 落在 $y$ 轴上时，求出 $t$ 的值．

查看试题解析

型号	载客量	租金单价
A	30人/辆	380元/辆
B	20人/辆	280元/辆