江西省九江市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 观察下列图形,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 则下列不等式不成立的是( )A、 B、 C、 D、3. 下列多项式能用公式法分解因式的是( )A、 B、 C、 D、4. 无论 为何值,下列分式一定有意义的是( )A、 B、 C、 D、5. 如图,将 沿 方向平移得到 ,若 的周长为 , 四边形 的周长为 ,则平移的距离为( )
2. 若 则下列不等式不成立的是( )A、 B、 C、 D、3. 下列多项式能用公式法分解因式的是( )A、 B、 C、 D、4. 无论 为何值,下列分式一定有意义的是( )A、 B、 C、 D、5. 如图,将 沿 方向平移得到 ,若 的周长为 , 四边形 的周长为 ,则平移的距离为( ) A、 B、 C、 D、6. 如图,四边形 的对角线 相交于点O, .添加下列条件能判定四边形 是平行四边形的是( )
A、 B、 C、 D、6. 如图,四边形 的对角线 相交于点O, .添加下列条件能判定四边形 是平行四边形的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
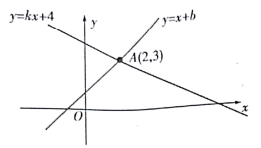
7. 四边形的内角和为 .8. 化简: .9. 在 中, 分别为 的中点,连接 ,则 的周长为 .10. 如图,直线 与直线 交于点 ,则关于 的不等式 的解集是 .
 11. 如图,把 绕点 顺时针旋转角度 得到,对应 ,若点 在边 上,且 ,则a= .
11. 如图,把 绕点 顺时针旋转角度 得到,对应 ,若点 在边 上,且 ,则a= . 12. 如图,在 中, ,对角线 交于点 ,点 从点 出发,沿着边 运动到点 停止,在点 运动过程中,若 是直角三角形,则 的长是 .
12. 如图,在 中, ,对角线 交于点 ,点 从点 出发,沿着边 运动到点 停止,在点 运动过程中,若 是直角三角形,则 的长是 .
三、解答题
-
13.(1)、因式分解:(2)、计算:14. 解不等式组: 并在数轴上表示它的解集.
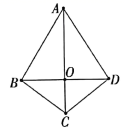
 15. 解分式方程:16. 如图,在四边形 中, ,对角线 相交于点 .
15. 解分式方程:16. 如图,在四边形 中, ,对角线 相交于点 .求证: 垂直平分线段 .
 17. 如图,依次连接四边形 四边的中点 ,得到的新四边形 是什么四边形?请证明.
17. 如图,依次连接四边形 四边的中点 ,得到的新四边形 是什么四边形?请证明.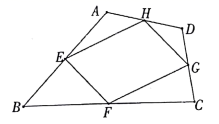 18. 解答下列问题:(1)、一正方形的面积是 ,则表示该正方形的边长的代数式是 .(2)、求证:当n为正整数时, 能被 整除.19. 如图,在 中, ,点 在 上,且 , ,垂足为E,连接BE.
18. 解答下列问题:(1)、一正方形的面积是 ,则表示该正方形的边长的代数式是 .(2)、求证:当n为正整数时, 能被 整除.19. 如图,在 中, ,点 在 上,且 , ,垂足为E,连接BE. (1)、求证: ;(2)、求 的度数.20. 某种学习用品,单价为 元/件,为促进消费,甲、乙两个商场均举行优惠活动甲商场优惠方案是:每件都按单价九折销售;乙商场优惠方案是:若不超过 件,每件按原价销售,若超过 件,超过的部分每件按原价八折销售设王老师购买学习用品件数为x.(1)、当 时,应该选择哪种方案更合算?(2)、若王老师到乙商场购买更合算,求 的取值范围.21. 如图,在平面直角坐标系中,点 的坐标为 ,等边三角形 经过平移或轴对称或旋转都可以得到 .
(1)、求证: ;(2)、求 的度数.20. 某种学习用品,单价为 元/件,为促进消费,甲、乙两个商场均举行优惠活动甲商场优惠方案是:每件都按单价九折销售;乙商场优惠方案是:若不超过 件,每件按原价销售,若超过 件,超过的部分每件按原价八折销售设王老师购买学习用品件数为x.(1)、当 时,应该选择哪种方案更合算?(2)、若王老师到乙商场购买更合算,求 的取值范围.21. 如图,在平面直角坐标系中,点 的坐标为 ,等边三角形 经过平移或轴对称或旋转都可以得到 .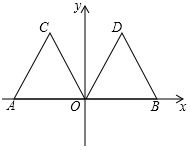 (1)、 沿 轴向右平移得到 ,则平移的距离是个单位长度;
(1)、 沿 轴向右平移得到 ,则平移的距离是个单位长度;与 关于直线对称,则对称轴是;
绕原点 顺时针旋转得到 ,则旋转角 是度 ;
(2)、 是平面内一点,若以 为顶点的四边形是平行四边形,直接写出点 的坐标.22. 疫情期间,人们的体温倍受关注某商场计划购进一批 两种型号的体温测量仪器,每台 种仪器价格比每台 种仪器价格多 元,花 元购买 种仪器和花 万元购买 种仪器的数量相同.(1)、求 两种仪器每台各多少元?(2)、根据销售情况,需要购进 两种仪器共 台,总费用不超过 万元,求 种仪器至少要购买多少台?(3)、若每台 种仪器售价为 元,每台 种仪器售价 元,在 的情况下商场应如何进货才能使这批体温测量仪器售完后获利最多?23. 定义:如果直线 且相邻的两条直线间距离相等.这样的一组平行线称为等距线,相邻的两直线间的距离记为d.(1)、探究:如图1.一条直线与一组等距线分别交于 三点,求证: .
 (2)、应用:
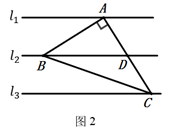
(2)、应用:如图2.等腰直角 的顶点 分别在等距线上 与 交于点 求 的值.
 (3)、如图3,等边 的顶点 分别在一组等距线中的 上, 分别交 于点 交 于点 当 时,求 的面积.
(3)、如图3,等边 的顶点 分别在一组等距线中的 上, 分别交 于点 交 于点 当 时,求 的面积.