江西省赣州市经开区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 若函数 中,y的值随x值的增大而减小,则k的取值范围为( )A、 B、 C、 D、3. 小红同学对数据24,48,23,24,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数4. 三个正方形的面积如图所示,则面积为 的正方形的边长为( )
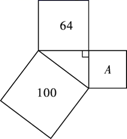 A、164 B、36 C、8 D、65. 若定义:f(a,b)=(-a,b),g(m,n)=(m,-n),例如f(1,2)=(-1,2),g(-4,-5)=(-4,5),则g(f(3,-4))的值为( )A、(3,-4) B、(-3,4) C、(3,4) D、(-3,-4)6. 如图,有一块边长为2 的正方形厚纸板ABCD,做成如图①所示的一套七巧板(点O为正方形纸板对角线的交点,点E,F分别为AD,CD的中点,CE∥BI,IH∥CD),将图①所示七巧板拼成如图②所示的“鱼形”,则“鱼尾”MN的长为( )
A、164 B、36 C、8 D、65. 若定义:f(a,b)=(-a,b),g(m,n)=(m,-n),例如f(1,2)=(-1,2),g(-4,-5)=(-4,5),则g(f(3,-4))的值为( )A、(3,-4) B、(-3,4) C、(3,4) D、(-3,-4)6. 如图,有一块边长为2 的正方形厚纸板ABCD,做成如图①所示的一套七巧板(点O为正方形纸板对角线的交点,点E,F分别为AD,CD的中点,CE∥BI,IH∥CD),将图①所示七巧板拼成如图②所示的“鱼形”,则“鱼尾”MN的长为( )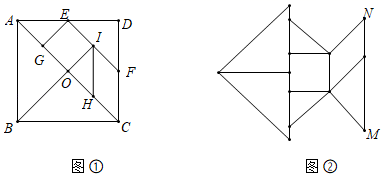 A、2 B、2 C、3 D、3
A、2 B、2 C、3 D、3二、填空题
-
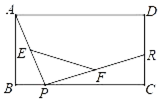
7. 若两个最简二次根式 与 能够合并,则m=。8. 一次函数 与 图象的交点是 ,则方程组 的解为 .9. 某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占30%,期末考试成绩占70%,小宁这个学期的期中、期末成绩(百分制)分别是80分、90分,则小宁这个学期的体育综合成绩是分10. 如图,已知矩形ABCD,P、R分别是BC和DC上的动点,E、F分别是PA、PR的中点.如果DR=5,AD=12,则EF的长为.
 11. 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,点C到AB边的距离为.
11. 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,点C到AB边的距离为. 12. 某市规定了每月用水不超过l8立方米和超过18立方米两种不同的收费标准,该市用户每月应交水费y(元)是用水x(立方米)的函数,其图象如图所示.已知小丽家3月份交了水费102元,则小丽家这个月用水量为立方米.
12. 某市规定了每月用水不超过l8立方米和超过18立方米两种不同的收费标准,该市用户每月应交水费y(元)是用水x(立方米)的函数,其图象如图所示.已知小丽家3月份交了水费102元,则小丽家这个月用水量为立方米.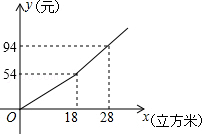
三、解答题
-
13. 计算题:(1)、(2)、14. 如图,用两个面积为 的小正方形拼成一个大的正方形.
 (1)、则大正方形的边长是;(2)、若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为5:4,且面积为 ?15. 如图,已知一次函数 的图象与 轴, 轴分别交于A,B两点,点 在该函数的图象上,连接OC.求点A,B的坐标和 的面积.
(1)、则大正方形的边长是;(2)、若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为5:4,且面积为 ?15. 如图,已知一次函数 的图象与 轴, 轴分别交于A,B两点,点 在该函数的图象上,连接OC.求点A,B的坐标和 的面积.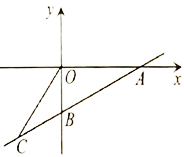 16. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,求这个风车的外围周长.
16. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,求这个风车的外围周长.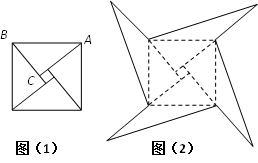 17. 如图,在四边形ABDC中,AB=AC,BD=DC,BE∥DC,请仅用无刻度的直尺按下列要求画图.
17. 如图,在四边形ABDC中,AB=AC,BD=DC,BE∥DC,请仅用无刻度的直尺按下列要求画图.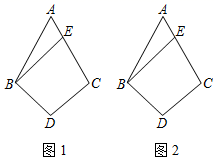 (1)、在图1中,画一个以AB为边的直角三角形;(2)、在图2中,画一个菱形,要求其中一边在BE上.18. 如图, 的对角线相交于点O,直线EF过点O分别交BC,AD于点E、F,G、H分别为OB、OD的中点,求证:四边形GEHF是平行四边形.
(1)、在图1中,画一个以AB为边的直角三角形;(2)、在图2中,画一个菱形,要求其中一边在BE上.18. 如图, 的对角线相交于点O,直线EF过点O分别交BC,AD于点E、F,G、H分别为OB、OD的中点,求证:四边形GEHF是平行四边形. 19. 在抗击新型冠状病毒疫情期间,某校学生主动发起为武汉加油捐款活动,为了了解学生捐款金额(单位:元),随机调查了该校的部分学生,根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
19. 在抗击新型冠状病毒疫情期间,某校学生主动发起为武汉加油捐款活动,为了了解学生捐款金额(单位:元),随机调查了该校的部分学生,根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: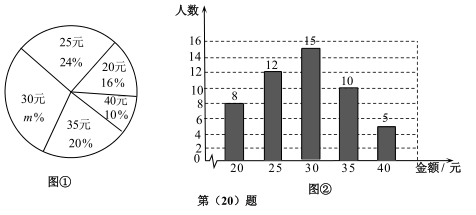 (1)、本次接受调查的学生人数为 , 图①中m的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的这组学生捐款数据的样本数据,若该校共有1800名学生,估计该校此次捐款总金额为多少元?20. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为 ,所以这个三角形是常态三角形.
(1)、本次接受调查的学生人数为 , 图①中m的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的这组学生捐款数据的样本数据,若该校共有1800名学生,估计该校此次捐款总金额为多少元?20. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为 ,所以这个三角形是常态三角形.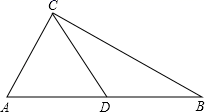 (1)、若 三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是” ;(2)、如图, 中, , ,点 为 的中点,连接 ,若 是常态三角形,求 的面积.21. 年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
(1)、若 三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是” ;(2)、如图, 中, , ,点 为 的中点,连接 ,若 是常态三角形,求 的面积.21. 年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:商品
价格
甲
乙
进件(元/个)
售价(元/个)
该店有一批用 元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共 元.[毛利润 (售价 进价) 销售量]

 (1)、该店库存的甲、乙两种手持红外测温枪分别为多少个?(2)、根据销售情况,该店计划增加甲种手持红外测温枪的购进量,减少乙种手持红外测温枪的购进量.已知甲种手持红外测温枪增加的数量是乙种手持红外测温枪减少的数量的 倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过 元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.22. 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)、该店库存的甲、乙两种手持红外测温枪分别为多少个?(2)、根据销售情况,该店计划增加甲种手持红外测温枪的购进量,减少乙种手持红外测温枪的购进量.已知甲种手持红外测温枪增加的数量是乙种手持红外测温枪减少的数量的 倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过 元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.22. 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.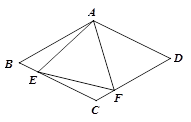 (1)、证明不论E、F在BC.CD上如何滑动,总有BE=CF;(2)、当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.23. 在平面直角坐标系之中,点O为坐标原点,直线 分别交x、y轴于点B、A,直线 与直线 交于点C.
(1)、证明不论E、F在BC.CD上如何滑动,总有BE=CF;(2)、当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.23. 在平面直角坐标系之中,点O为坐标原点,直线 分别交x、y轴于点B、A,直线 与直线 交于点C.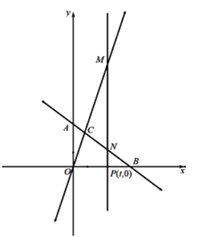
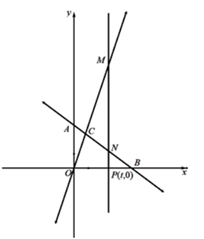
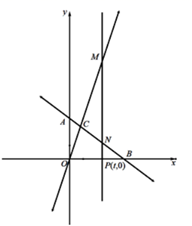
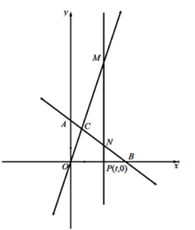 (1)、如图1,求点C的坐标.(2)、如图2,点P(t,0)为C点的右侧x轴上一点,过点P作x轴垂线分别交AB、OC于点N、M,若MN=5NP,求t的值.(3)、如图3,点F为平面内任意一点,是否存在y轴正半轴上一点E,使点E、F、M、N围成的四边形为菱形,若存在求出点E坐标;若不存在,请说明理由.
(1)、如图1,求点C的坐标.(2)、如图2,点P(t,0)为C点的右侧x轴上一点,过点P作x轴垂线分别交AB、OC于点N、M,若MN=5NP,求t的值.(3)、如图3,点F为平面内任意一点,是否存在y轴正半轴上一点E,使点E、F、M、N围成的四边形为菱形,若存在求出点E坐标;若不存在,请说明理由.