福建省泉州市永春县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 点P(2,3)到 轴的距离是( )A、5 B、3 C、2 D、12. 计算 的结果为( )A、 B、 C、 D、3. 平行四边形ABCD中,∠A=50°,则∠B的度数是( )A、40° B、50° C、130° D、150°4. 方程 的解是( )A、 B、 C、 D、5. 已知菱形ABCD的对角线AC、BD的长分别为4和6,则该菱形面积是( )A、48 B、24 C、12 D、66. 如图,矩形ABCD的对角线AC与BD相交于点O,∠AOD=60°,AD=8,则△BOC的周长是( )
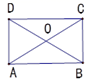 A、16 B、24 C、30 D、207. 在一次函数 中, 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、8. 如图,在平行四边形ABCD中,AB=5,BE平分∠ABC交CD边于点E,且DE=2,则BC的长为( )
A、16 B、24 C、30 D、207. 在一次函数 中, 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、8. 如图,在平行四边形ABCD中,AB=5,BE平分∠ABC交CD边于点E,且DE=2,则BC的长为( )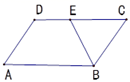 A、6 B、5 C、4 D、39. 如图,L1: 与L2: 相交于点P( ,4),则关于 的不等式 的解集为( )
A、6 B、5 C、4 D、39. 如图,L1: 与L2: 相交于点P( ,4),则关于 的不等式 的解集为( )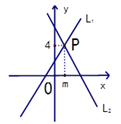 A、 B、 C、 D、10. 如图,已知菱形OABC,OC在 轴上,AB交 轴于点D,点A在反比例函数 上,点B在反比例函数 上,OD=2,则 的值为( )
A、 B、 C、 D、10. 如图,已知菱形OABC,OC在 轴上,AB交 轴于点D,点A在反比例函数 上,点B在反比例函数 上,OD=2,则 的值为( )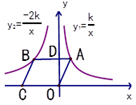 A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
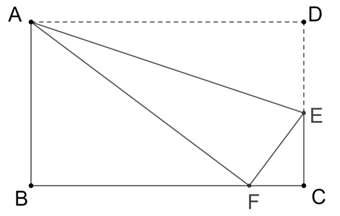
11. 若分式 在实数范围内有意义,则x的取值范围是 .12. 某种细菌病毒的直径为0.00005米,0.00005米用科学记数法表示为米.13. 甲、乙两人进行射击测试,每人射击10次.射击成绩的平均数相同,射击成绩的方差分别为S甲2=5,S乙2=3.5,则射击成绩比较稳定的是(填“甲”或“乙“).14. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,则EF的长度是 .
 15. 将直线 的图象向下平移3个单位后,经过点A(3,-4),则平移后的直线解析式为 .16. 如图,直线 与双曲线 相交于A、B两点,以AB为边作正方形ABCD,则正方形ABCD面积的最小值为 .
15. 将直线 的图象向下平移3个单位后,经过点A(3,-4),则平移后的直线解析式为 .16. 如图,直线 与双曲线 相交于A、B两点,以AB为边作正方形ABCD,则正方形ABCD面积的最小值为 .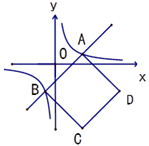
三、解答题
-
17. 计算: .18. 先化简,再求值 , 其中 .19. 学校举行信息技术应用大赛,将八年级50名学生参加竞赛的成绩统计后,绘制成如下成绩统计表.
组别
A组
B组
C组
D组
成绩 (分)
60≤ <70
70≤ <80
80≤ <90
90≤ <100
人数
10
20
16
4
组平均分(分)
66
74
85
95
观察上面的图表,解答下列问题:
(1)、成绩的中位数落在哪一个组别?(2)、求八年级参加竞赛学生的平均成绩.20. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同,现在平均每天生产多少台机器?21. 如图,平行四边形ABCD的对角线交于点O,且AB=13,AC=24,BD=10.求证:四边形ABCD是菱形.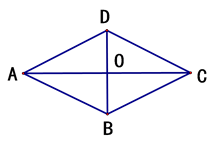 22. 轿车和货车从同时从甲地出发驶往乙地,轿车到达乙地后立即返回甲地,货车到达乙地后停止.如图所示, 、 分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.
22. 轿车和货车从同时从甲地出发驶往乙地,轿车到达乙地后立即返回甲地,货车到达乙地后停止.如图所示, 、 分别表示货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系.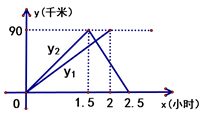 (1)、求 与 之间的函数关系式;(2)、当轿车从乙地返回甲地的途中与货车相遇时,求相遇处到甲地的距离.23. 如图,在正方形ABCD中,点E为线段BC上一动点(点E不与点B、C重合),点B关于直线AE的对称点为F,作射线EF交CD于H,连接AF.
(1)、求 与 之间的函数关系式;(2)、当轿车从乙地返回甲地的途中与货车相遇时,求相遇处到甲地的距离.23. 如图,在正方形ABCD中,点E为线段BC上一动点(点E不与点B、C重合),点B关于直线AE的对称点为F,作射线EF交CD于H,连接AF.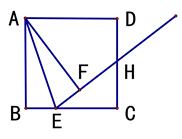 (1)、求证:AF⊥EH;(2)、连接AH,小王通过观察、实验,提出猜想:点E在运动过程中,∠EAH的度数始终保持不变.你帮助小王求出∠EAH的度数.24. 某商店购买30件A商品和20件B商品共用了680元,购买10件A商品和10件B商品共用了260元.(1)、A、B两种商品的单价分别是多少元?(2)、商店准备购买A、B两种商品共100件(其中购买A种商品m件),要求购买A商品的数量不少于B商品数量的 ,且总费用不超过1250元.
(1)、求证:AF⊥EH;(2)、连接AH,小王通过观察、实验,提出猜想:点E在运动过程中,∠EAH的度数始终保持不变.你帮助小王求出∠EAH的度数.24. 某商店购买30件A商品和20件B商品共用了680元,购买10件A商品和10件B商品共用了260元.(1)、A、B两种商品的单价分别是多少元?(2)、商店准备购买A、B两种商品共100件(其中购买A种商品m件),要求购买A商品的数量不少于B商品数量的 ,且总费用不超过1250元.①该商店有几种购买方案?
②实际购买时A种商品每件下降 ( )元,B种商品每件上涨3 元,当购买这两种商品所需的最少费用为1248元时,求 的值.
25. 如图,矩形ABCD中,AB=4,AD=3,∠A的角平分线交边CD于点E.点P从点A出发沿射线AE以每秒2个单位长度的速度运动,Q为AP的中点,过点Q作QH⊥AB于点H,在射线AE的下方作平行四边形PQHM(点M在点H的右侧),设P点运动时间为 秒.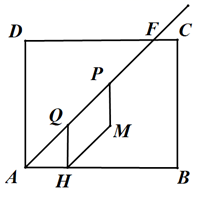
 (1)、写出 的面积(用含 的代数式表示).(2)、当点M落在BC边上时,求 的值.(3)、在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的 的值;若不存在请说明理由(不能添加辅助线).
(1)、写出 的面积(用含 的代数式表示).(2)、当点M落在BC边上时,求 的值.(3)、在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的 的值;若不存在请说明理由(不能添加辅助线).