福建省福州市2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-17 类型：期末考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x - 2}$ 有意义，x的值可以是（）

A、2 B、1 C、0 D、-1

查看试题解析
2. 一次函数y=﹣2x+3的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{2} = 2$ B、 $\sqrt{2} \times \sqrt{2} = 2$ C、 ${(\sqrt{2})}^{2} = 2 \sqrt{2}$ D、 $2 + \sqrt{2} = 2 \sqrt{2}$

查看试题解析
4. 在数据： 1，3，3，4，5， 6中，下列统计量所代表的值是3的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
5. 如图，在菱形ABCD中，对角线AC， BD相交于点O．下列结论不一定成立的是（）

A、BD平分∠ADC B、AC=BD C、AC⊥BD D、OA=OC

查看试题解析
6. 小明用刻度不超过100℃的温度计来估计某食用油的沸点温度，将该食用油倒入锅中，均匀加热，每隔10 s测量一次锅中的油温，得到如下数据：

时间t（单位：s）

0

10

20

30

40

油温y（单位：℃）

10

30

50

70

90

当加热100s时，油沸腾了，则小明估计这种油的沸点温度是（）

A、150℃ B、170℃ C、190℃ D、210℃

查看试题解析
7. 如图，在矩形ABCD中，对角线AC， BD相交于点O，若边AB的长不变，边BC的长逐渐增大，下列说法正确的是（）

A、边CD的长也逐渐增大 B、∠AOB也逐渐增大 C、边OD的长也逐渐增大 D、∠ACB也逐渐增大

查看试题解析
8. 下面的统计表描述了某车间工人日加工零件数的情况，这些工人日加工零件数的中位数是（）

日加工零件数

3

4

5

6

7

8

人数

4

5

8

9

6

4

A、5 B、6 C、5.5 D、9

查看试题解析
9. 已知 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ 是直线 $y = (m - 1) x + 3$ 上的相异两点，若 $(x_{1} - x_{2}) (y_{1} - y_{2}) < 0$ ，则m的取值范围是（）

A、 $m > 1$ B、 $m < 1$ C、 $m \geq 1$ D、 $m \leq 1$

查看试题解析
10. 若 $a = 2019 \times 2021 - 2019 \times 2020$ ， $b = \sqrt{2022^{2} - 4 \times 2021}$ ， $c = \sqrt{2020^{2} + 20}$ ，则a，b，c的大小关系是（）

A、 $a < b < c$ B、 $a < c < b$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析

二、填空题

11. 如图，A，B两点被池塘隔开，在AB外选一点C，连接AC和BC，分别取AC， BC的中点D，E，量得DE的长为25米，则AB的长是米．

查看试题解析
12. 已知直角三角形的两直角边长分别为3和5，则第三边的长是．

查看试题解析
13. 甲，乙两地7月上旬的日平均气温如图所示，则甲，乙两地这10天中日平均气温的方差 $S_{甲}^{2}$ 与 $S_{乙}^{2}$ 的大小关系是 $S_{甲}^{2}$ $S_{乙}^{2}$ （填“>”或“<”）．

查看试题解析
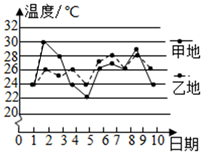14. 已知 $▱ A B C D$ 中，若∠A+∠C= 220，则∠B的度数是度．

查看试题解析
15. 在Rt△ABC中，∠BAC=90°，且a+c=9，a-c=4，则b的值是．

查看试题解析
16. 如图1，正方形ABCD的边长为4 cm， E为AB边上一点，连接DE，点P从点D出发，沿D→E→B以1 cm/s的速度匀速运动到点B．图2是△PCD的面积y （单位： cm²）随时间x （单位： s）的变化而变化的图象，其中0≤x≤b，则b的值是．

查看试题解析

三、解答题

17. 计算： $\sqrt{8} - {(\sqrt{2})}^{0} + {(\sqrt{2} - 1)}^{2}$ ．

查看试题解析
18. 已知一次函数y=kx+2 （k≠0）的图象经过点（1， 4）．

(1)、求该函数的解析式并画出图象；

(2)、根据图象，直接写出当y≤0时x的取值范围．

查看试题解析
19. 如图，点A， B分别在∠MON的两条边OM， ON上．

(1)、尺规作图：过点B在∠MON内部作射线BC// OM，并在BC上截取BD= OA；（保留作图痕迹，不写作法）

(2)、连接AD， OD， AB，若OA= OB， OD=8， AB= 6，求△ABD的面积．

查看试题解析
20. 水池中有水，水面是一个边长为10尺的正方形，水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的终点，它的顶端恰好到达池边的水面．水的深度和这根芦苇的长度分别是多少？

查看试题解析
21. 如图， $▱ A B C D$ 的对角线AC， BD相交于点O，将△ABO平移到△DCE，已知AO= 1， BO=2， $A B = \sqrt{5}$ ，求证：四边形OCED是矩形．

查看试题解析
22. 小林经营一家水果店，准备对店里的旺季水蜜桃开展一周的礼盒包装促销活动，其中8斤装的礼盒单价为60元，10 斤装的礼盒单价为68元.若每斤水蜜桃的进价为5元，每个礼盒的包装成本为2元．预估这两种包装的水蜜桃礼盒均有顾客购买，且会售出30盒，其中8斤装的礼盒数不多于10斤装的礼盒数的一半．

(1)、设8斤装的礼盒有x盒，这30盒水蜜桃售出的利润为y元，求y与x的关系式；

(2)、在（1）的情况下，8斤装的礼盒数x为何值时这30盒水蜜桃售出的利润最大?并求出利润的最大值：

查看试题解析

23. 某家庭为了解某品牌节水龙头的节水效果，记录了未使用节水龙头一个月（30天）的日用水量（单位：t）和使用该节水龙头一个月（30 天）的日用水量，得到如下图表：

未使用节水龙头的日用水量频数分布表

组别	日用水量x（单位：t）	频数
第一组	$0 \leq x < 0.2$	1
第二组	$0.2 \leq x < 0.4$	2
第三组	$0.4 \leq x < 0.6$	7
第四组	$0.6 \leq x < 0.8$	13
第五组	$0.8 \leq x < 1.0$	6
第六组	$1.0 \leq x < 1.2$	1

(1)、估计该家庭记录的未使用节水龙头的日用水量的平均数；

(2)、估计该家庭使用节水龙头后，一年能节省多少吨水? （一年按365天计算）

查看试题解析

24. 在平面直角坐标系xOy中，直线l₁经过A（0， 2）， B（1， 0）两点，直线l₂的解析式是y=kx+k （k≠0）．

(1)、求直线l₁的解析式；

(2)、试说明直线l₂必经过定点，并求出该定点的坐标；

(3)、将线段AB沿某个方向平移得到线段EF，其中E是点A的对应点．设点E的坐标为（m， n），若点F在直线l₂上，试说明点（-2， 2）在n关于m的函数图象上．

查看试题解析
25. 如图，正方形ABCD中， $A B = \sqrt{5}$ ，在边CD的右侧作等腰三角形DCE，使DC=DE，记∠CDE为a （0°<a<90°），连接AE，过点D作DG⊥AE，垂足为G，交EC的延长线于点F，连接AF．

(1)、求∠DEA的大小（用 $α$ 的代数式表示）；

(2)、求证：△AEF为等腰直角三角形；

(3)、当 $C F = \sqrt{2}$ 时，求点E到CD的距离．

查看试题解析

时间t（单位：s）	0	10	20	30	40
油温y（单位：℃）	10	30	50	70	90

日加工零件数	3	4	5	6	7	8
人数	4	5	8	9	6	4