北京市昌平区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,未来在亚太地区定位精度将优于5米,测速精度优于0.1米/秒,授时精度优于10纳秒,10纳秒为0.00000001秒,0.00000001用科学记数法表示为( )A、0.1×10﹣7 B、1×10﹣8 C、1×10﹣7 D、0.1×10﹣82. 不等式2x≥8的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、a2+a3=a5 B、(ab2)3=ab6 C、(﹣a2)3=a6 D、a2•a3=a54. 为了加强学生垃圾分类意识,提高学生垃圾分类能力,某校从全校2000名学生的垃圾分类知识测试卷中随机抽取了200份试卷进行成绩统计,在这个问题中以下说法正确的是( )A、200份试卷的成绩是样本 B、每名学生是个体 C、此调查为全面调查 D、样本容量是20005. 如图,直线l与直线a、b分别相交,且a∥b , ∠1=110°,则∠2的度数是( )
3. 下列运算正确的是( )A、a2+a3=a5 B、(ab2)3=ab6 C、(﹣a2)3=a6 D、a2•a3=a54. 为了加强学生垃圾分类意识,提高学生垃圾分类能力,某校从全校2000名学生的垃圾分类知识测试卷中随机抽取了200份试卷进行成绩统计,在这个问题中以下说法正确的是( )A、200份试卷的成绩是样本 B、每名学生是个体 C、此调查为全面调查 D、样本容量是20005. 如图,直线l与直线a、b分别相交,且a∥b , ∠1=110°,则∠2的度数是( )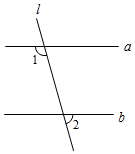 A、20° B、70° C、90° D、110°6. 已知 ,下列不等式变形错误的是( )A、 B、 C、 D、7. 分解因式2x2﹣8结果正确的是( )A、2(x+2)(x﹣2) B、2(x﹣2)2 C、2(x2﹣8) D、2(x+2)28. 如图,四边形ABCD , AC、BD交于点O , 0°<∠ABC<90°,AB∥CD , AD∥BC , 下列结论正确的是( )
A、20° B、70° C、90° D、110°6. 已知 ,下列不等式变形错误的是( )A、 B、 C、 D、7. 分解因式2x2﹣8结果正确的是( )A、2(x+2)(x﹣2) B、2(x﹣2)2 C、2(x2﹣8) D、2(x+2)28. 如图,四边形ABCD , AC、BD交于点O , 0°<∠ABC<90°,AB∥CD , AD∥BC , 下列结论正确的是( )①∠AOD=∠BOC;②∠DAC=∠BCA;③∠BAD+∠ABC=180°;④∠ABC=∠ADC .
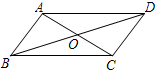 A、①② B、①②④ C、①②③ D、①②③④
A、①② B、①②④ C、①②③ D、①②③④二、填空题
-
9. 用不等式表示“x的2倍与3的差不小于0” .10. 已知∠A=30°,则∠A的余角为°.11. 计算:(6x2+4x)÷2x= .12. 写出一个二元一次方程组 , 使它的解是 .13. 分解因式:x3﹣2x2+x= .14. 计算:(2x+1)(x﹣2)= .15. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为.16. 观察、归纳:
(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;
…
请你根据以上等式的规律,完成下列问题:
⑴(x﹣1)(xn+…+x2+x+1)=﹣1;
⑵计算:1+2+22+…+22019= .
三、解答题
-
17. 计算:32﹣(3﹣π)0+2﹣1﹣|﹣ |.18. 解不等式:2x+1<10﹣x .19. 解方程组: .20. 解不等式组: ,并把它的解集在数轴上表示出来.
 21. 已知2x2﹣2x=1,求代数式(x﹣1)2+(x﹣3)(x+3)的值.22. 补全解答过程:
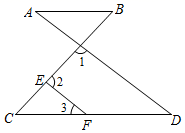
21. 已知2x2﹣2x=1,求代数式(x﹣1)2+(x﹣3)(x+3)的值.22. 补全解答过程:如图,∠1+∠2=180°,∠3=∠A .
求证:∠B=∠C .
证明:∵∠1+∠2=180°,
∴(同旁内角互补,两直线平行).
∴∠3=∠D().
又∵∠3=∠A ,
∴ .
∴AB∥CD().
∴∠B=∠C().
 23. 已知关于x、y的二元一次方程y=kx+b(k、b为常数)的正整数解如表所示:
23. 已知关于x、y的二元一次方程y=kx+b(k、b为常数)的正整数解如表所示:y=kx+b
x
1
2
3
y
5
3
1
求k和b的值.
24. 问题:调查、分析某校七年级(2)班学生完整阅读中国古代四大名著的数目.调査目的:了解该班学生阅读中国四大名著数目,为后续指导阅读提供依据.
调查范围:七年级(2)班全体学生.
调查方法:实地调查法.
数据的整理与表示:
某校七年级(2)班学生完整阅读中国四大名著数目统计表
完整阅读的数目
4
3
2
1
人数
m
10
2
2

问题:
(1)、表格中m的值为;(2)、阅读4本扇形圆心角的度数为°;(3)、求七年级(2)班学生平均阅读中国四大名著的数目;(4)、完整阅读中国古代四大名著数目的众数为本;(5)、完整阅读中国古代四大名著数目的中位数为本.25. 七年级某班现有班费45元,计划购买甲、乙两种小礼品共10件作为班级主题班会学生活动的奖品,它们的单价分别为4元、5元.若45元班费正好用完,求甲、乙两种小礼品各购买多少件.26. 小明和小亮玩纸片拼图游戏,发现利用图1中的三种材料各若干可以拼出一些长方形来解释某些等式.例如图2可以解释的等式为(a+2b)(a+b)=a2+3ab+2b2 .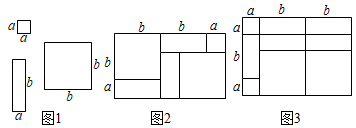 (1)、图3可以解释的等式为;(2)、请你利用图1中的三种材料各若干拼出一个正方形来解释(a+b)2=a2+2ab+b2 , 画出你拼出的正方形示意图;(3)、要拼出一个长为a+3b , 宽为2a+b的长方形,需要如图1所示的边长为a的正方形纸片块,长为b , 宽为a的长方形纸片块,边长为b的正方形纸片块.27. 如图,CE是∠ACD的平分线,过点A作CD的平行线交CE于点B .
(1)、图3可以解释的等式为;(2)、请你利用图1中的三种材料各若干拼出一个正方形来解释(a+b)2=a2+2ab+b2 , 画出你拼出的正方形示意图;(3)、要拼出一个长为a+3b , 宽为2a+b的长方形,需要如图1所示的边长为a的正方形纸片块,长为b , 宽为a的长方形纸片块,边长为b的正方形纸片块.27. 如图,CE是∠ACD的平分线,过点A作CD的平行线交CE于点B .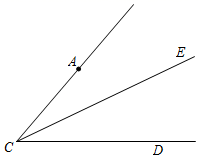 (1)、补全图形;(2)、求证:∠ACB=∠ABC;(3)、点P是射线CE上的一点(点P不与点B和点C重合),连接AP , ∠PCD=α,∠PAB=β,∠APC=γ,请直接写出α,β与γ之间的数量关系.28. 如图,数轴上两点A、B对应的数分别是﹣1,1,点P是线段AB上一动点,给出如下定义:如果在数轴上存在动点Q , 满足|PQ|=2,那么我们把这样的点Q表示的数称为连动数,特别地,当点Q表示的数是整数时我们称为连动整数.
(1)、补全图形;(2)、求证:∠ACB=∠ABC;(3)、点P是射线CE上的一点(点P不与点B和点C重合),连接AP , ∠PCD=α,∠PAB=β,∠APC=γ,请直接写出α,β与γ之间的数量关系.28. 如图,数轴上两点A、B对应的数分别是﹣1,1,点P是线段AB上一动点,给出如下定义:如果在数轴上存在动点Q , 满足|PQ|=2,那么我们把这样的点Q表示的数称为连动数,特别地,当点Q表示的数是整数时我们称为连动整数.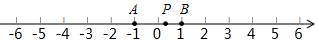 (1)、﹣3,0,2.5是连动数的是;(2)、关于x的方程2x﹣m=x+1的解满足是连动数,求m的取值范围;(3)、当不等式组 的解集中恰好有4个解是连动整数时,求a的取值范围.
(1)、﹣3,0,2.5是连动数的是;(2)、关于x的方程2x﹣m=x+1的解满足是连动数,求m的取值范围;(3)、当不等式组 的解集中恰好有4个解是连动整数时,求a的取值范围.