上海市松江区2019-2020学年七年级下学期数学期末试卷
试卷更新日期：2020-09-16 类型：期末考试
一、单选题
-
1. 下列等式中，正确的有（ ）A、 B、 C、 D、2. 如图，在下列条件中，能说明AC∥DE的是（ ）
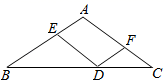A、∠A＝∠CFD B、∠BED＝∠EDF C、∠BED＝∠A D、∠A+∠AFD＝180°3. 利用尺规作∠AOB的角平分线OC的作图痕迹如图所示，说明∠AOC＝∠BOC用到的三角形全等的判定方法是（ ）
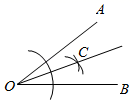A、SSS B、SAS C、ASA D、AAS4. 如图，关于△ABC ， 给出下列四组条件：①△ABC中，AB＝AC；
②△ABC中，∠B＝56°，∠BAC＝68°；
③△ABC中，AD⊥BC ， AD平分∠BAC；
④△ABC中，AD⊥BC ， AD平分边BC ．
其中，能判定△ABC是等腰三角形的条件共有（ ）
A、1组 B、2组 C、3组 D、4组二、填空题
-
5. 16的平方根是 ，9的立方根是 ．6. = ．7. 比较大小：2（填“＞”或“＜”或“=”）
8. 请写出一个大于1且小于2的无理数：.9. 截止2020年6月5日，全世界感染新冠肺炎的人数约为6650000人，数字6650000用科学记数法表示，并保留2个有效数字，应记为 ．10. 一个实数在数轴上对应的点在负半轴上，且到原点距离等于 ，则这个数为 ．11. 在平面直角坐标系中，将点A（﹣3，﹣1）向右平移3个单位后得到的点的坐标是 ．12. 在平面直角坐标系中，点P（m+3，m+1）在y轴上，则m＝ ．13. 已知：如图，直线a∥b ， 直线c与a ， b相交，若∠2＝115°，则∠1＝度．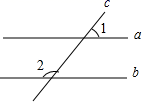
14. 如图所示，AD∥BC ， BD平分∠ABC ， 若∠A=110°，则∠D=.
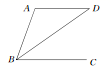15. 已知等腰三角形的两条边长分别是3cm、7cm，那么这个等腰三角形的周长是 cm．16. 如图，直线a∥b ， 点A ， B位于直线a上，点C ， D位于直线b上，且AB：CD＝1：2，如果△ABC的面积为10，那么△BCD的面积为 ．
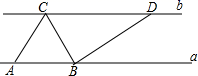17. 如图，在△ABC中，两个内角∠BAC与∠BCA的角平分线交于点D ， 若∠B＝70°，则∠D＝度．
18. 如图，在△ABC中，∠A＝100度，如果过点B画一条直线l能把△ABC分割成两个等腰三角形，那么∠C=度．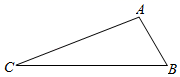
三、解答题
-
19. 计算：3÷ ﹣ +（ ）﹣1﹣（ +2）0 ．20. 计算：21. 在△ABC中，已知∠A：∠B：∠C＝2：3：5，求∠A、∠B、∠C的度数．22. 如图，已知 AD∥BC ， 点E是AD的中点，EB＝EC ． 试说明AB与CD相等的理由．
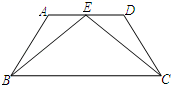23. 如图，已知DE∥BC ， EF平分∠CED ， ∠A＝∠CFE ， 那么EF与AB平行吗？为什么？解：因为DE∥BC（已知），
所以∠DEF＝∠CFE（），
因为 （已知），
所以∠DEF＝∠CEF（角平分线的意义），
所以∠ ＝∠CEF（等量代换），
因为∠A＝∠CFE（已知），
所以∠A＝（），
所以EF∥AB（）．
24. 在平面直角坐标系中，已知点A的坐标为（3，2）．设点A关于y轴的对称点为B ， 点A关于原点O的对称点为C ， 点A绕点O顺时针旋转90°得点D ．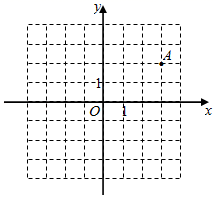
(1)、点B的坐标是；点C的坐标是；
点D的坐标是；
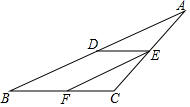
(2)、顺次联结点A、B、C、D ， 那么四边形ABCD的面积是 ．25. 如图，已知在△ABC中，点D为AC边上一点，DE∥AB交边BC于点E ， 点F在DE的延长线上，且∠FBE＝∠ABD ， 若∠DEC＝∠BDA ．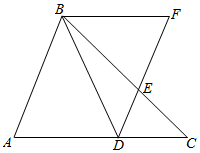
(1)、试说明∠BDA＝∠ABC的理由；(2)、试说明BF∥AC的理由．26. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC ， 点D在边BC上（不与点B、C重合），BE⊥AD ， 重足为E ， 过点C作CF⊥CE ， 交线段AD于点F ．
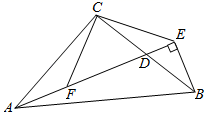(1)、试说明△CAF≌△CBE的理由；(2)、数学老师在课堂上提出一个问题，如果EF＝2AF ， 试说明CD＝BD的理由．班级同学随后进行了热烈讨论，小明同学提出了自己的想法，可以取EF的中点H ， 联结CH ， 就能得出结论，你能否能根据小明同学的想法，写出CD＝BD的理由．27. 如图，在等边△ABC中，已知点E在直线AB上（不与点A、B重合），点D在直线BC上，且ED＝EC ．
(1)、若点E为线段AB的中点时，试说明DB＝AE的理由；(2)、若△ABC的边长为2，AE＝1，求CD的长．