北京市门头沟区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-16 类型：期末考试

进入出卷网下载

一、单选题

1. 把不等式 x ≤1 的解集表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
2. 计算 a²×a³ 的结果是（）

A、a⁶ B、a⁵ C、2a⁵ D、a⁹

查看试题解析
3. 空气的密度是 0.00129 克每立方厘米，将 0.00129 用科学记数法表示应为（）

A、1.29 ´10^-³ B、1.29 ´10^-⁵ C、1.29 ´10^-⁴ D、1.29 ´10^-²

查看试题解析
4. 下列事件中，必然事件是（）

A、任意掷一枚均匀的硬币，正面朝上 B、通常情况下，抛出的篮球会下落 C、从一副扑克牌中，随意抽出一张是大王 D、三角形内角和为 360°

查看试题解析
5. 如图，直线 AB ， CD 交于点 O ，射线 OM 平分∠AOC ，如果∠AOD = 104°，那么∠BOM 等于（）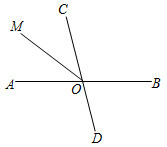

A、38° B、104° C、140° D、142°

查看试题解析
6. 如果 a ＞ b ，那么下列不等式变形正确的是（）

A、a + 5 ＜ b + 5 B、 $\frac{a}{3} < \frac{b}{3}$ C、-4a ＞ - 4b D、a - 2 ＞ b - 2

查看试题解析
7. 右图是某市10月1日至7日一周内“日平均气温变化统计图”．在这组数据中，众数和中位数分别是（）

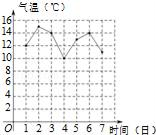A、13，13 B、14，14 C、13，14 D、14，13

查看试题解析
8. 近年来，某市旅游事业稳步发展，下面是根据该市旅游网提供的数据制成的 2016 年～2019年旅游总人数和旅游总收入同比增长率统计图：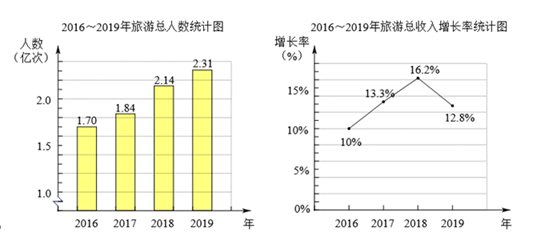

下面有三个推断：

① 从 2016 年到 2019 年，年旅游总人数增长最多的是 2018 年，比上一年增长了 0.3 亿人次；

② 从 2016 年到 2019 年，年旅游总收入最高的是 2018 年；

③ 如果 2016 年旅游总收入为 2 442.1 亿元，那么 2015 年旅游总收入约为 2 220 亿元．其中所有合理的推断的序号是（）

A、①② B、②③ C、①③ D、①②③

查看试题解析

二、填空题

9. 计算： (p - 5)⁰= （）．

查看试题解析
10. 如果把方程3x+y＝2写成用含x的代数式表示y的形式，那么y＝．

查看试题解析
11. 写出方程 x - y = 1 的一个整数解为．

查看试题解析
12. 如图中的四边形均为长方形，根据图形，写出一个正确的等式：.

查看试题解析
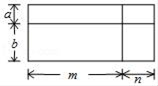13. 《算法统宗》是中国古代数学名著，作者是明代著名数学家程大位．在其中有这样的记载“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”译文：有100名和尚分100个馒头，正好分完．如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚各有几人？设有大和尚x人，小和尚y人，可列方程组为．

查看试题解析
14. 关于x的不等式 $a x > b$ 的解集是 $x < \frac{a}{b}$ ，写出一组满足条件的a ， b的值：a= ， b= ．

查看试题解析
15. 如图，点O为直线AB上一点，OC⊥OD ，如果∠1＝35°，那么∠2的度数是；

查看试题解析
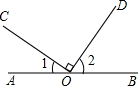16. 学完一元一次不等式解法后，老师布置了如下练习：
解不等式 $\frac{15 - 3 x}{2} \geq 7 - x$ ，并把它的解集在数轴上表示出来．

以下是小明的解答过程：

解：第一步去分母，得15 - 3x≥2(7 - x) ，

第二步去括号，得15 - 3x≥14 - 2x ，

第三步移项，得

-3x + 2x≥14 - 15 ，

第四步合并同类项，得-x≥ - 1 ，

第五步系数化为 1，得x≥1．

第六步把它的解集在数轴上表示为：

老师看后说：“小明的解题过程有不符合题意！”

问：请指出小明从第几步开始出现了不符合题意，并说明判断依据．

答：．

查看试题解析

三、解答题

17. 把下列各式分解因式：

(1)、6x⁴ - 12x²z

(2)、2x² - 18

查看试题解析
18. 计算：

(1)、(a + b)(a - b) - a²

(2)、(a + 2)(a - 3) + ${(a + 2)}^{2}$

查看试题解析
19. 如图，点 P 是∠ ABC 内一点.

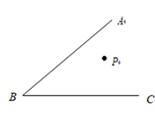(1)、过点 P 画 BC 的垂线，垂足为点 D；

(2)、过点 P 画 BC 的平行线交 AB 于点 E；

(3)、如果∠ B = 40°，那么∠ PEB =°

查看试题解析
20. 解方程组： ${\begin{array}{l} 2 x - 3 y = 3 \\ 3 x - 2 y = 7 \end{array}$

查看试题解析
21. 先化简，再求值：
[(2x - y )² + x ( y - 4x) + 8 y² ]÷3y ，其中 x = 3 ， y = -1

查看试题解析
22. 解不等式组 ${\begin{array}{l} 4 (x + 1) \leq 7 x + 10 \\ x - 5 < \frac{x - 8}{3} \end{array}$ 并求出这个不等式组的所有的正整数解．

查看试题解析
23. 完成下面的证明：

(1)、已知：如图，AB∥CD
求证：∠1+∠3 = 180°

证明：∵ AB∥CD（已知），

∴ ∠1+∠2 = 180°（）

又∵ ∠2 = ∠3（）

∴ ∠1+∠3=180°（）

(2)、已知：如图，AM∥EF ， ∠1 = ∠B ．
求证：∠2 = ∠C ．

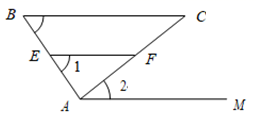
证明：∵ ∠1 = ∠B（已知），

∴ EF∥BC（）

∵ AM∥EF（已知），

∴ AM∥BC（）

∴ ∠2 = ∠C（）

查看试题解析
24. 为响应国家“低碳环保，绿色出行”的号召，区政府基于“服务民生”理念，运用信息化管理与服务手段，为居住区和旅游景点等人流量集中的地区提供公共自行车服务的智能交通系统. 小明针对某校七年级学生（共 16 个班，480 名学生）每月使用公共自行车的次数进行了调查．

(1)、小明采取的下列调查方式中，比较合理的是；理由是：
A．对七年级（1）班的全体同学进行问卷调查

B．对七年级各班的班长进行问卷调查

C．对七年级各班学号为 3 的倍数的全体同学进行问卷调查

(2)、小明根据问卷调查的结果绘制了如下两幅不完整的统计图，根据图中提供的信息解答下列问题：
① 在扇形统计图中“10次以下”所在的扇形的圆心角等于度；

② 补全条形统计图；

③ 根据调查结果，估计七年级每月使用公共自行车次数是“16 至 20 次”的同学有人．

查看试题解析
25. 已知：如图，在三角形 ABC 中，点 E、G 分别在 AB 和 AC 上．EF⊥BC 于点 F ， AD⊥BC 于点 D ，连接 DG. 如果∠1 = ∠2，请猜想 AB 与 DG 的位置关系，并证明你的猜想．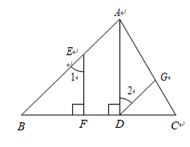

查看试题解析
26. 2017年5月31日，昌平区举办了首届初二年级学生“数学古文化阅读展示”活动，为表彰在本次活动中表现优秀的学生，老师决定在6月1日购买笔袋或彩色铅笔作为奖品. 已知1个笔袋、2筒彩色铅笔原价共需44元；2个笔袋、3筒彩色铅笔原价共需73元.

(1)、每个笔袋、每筒彩色铅笔原价各多少元？

(2)、时逢“儿童节”，商店举行“优惠促销”活动，具体办法如下：笔袋“九折”优惠；彩色铅笔不超过10筒不优惠，超出10筒的部分“八折”优惠. 若买x个笔袋需要y₁元，买x筒彩色铅笔需要y₂元. 请用含x的代数式表示y₁、y₂；

(3)、若在（2）的条件下购买同一种奖品95件，请你分析买哪种奖品省钱.

查看试题解析
27. 如果 x 是一个有理数，我们定义{x} 表示不小于 x 的最小整数．如{3.2} = 4 ， {-2.6} = -2 ， {5} = 5 ， {-6} = -6.由定义可知，任意一个有理数都能写成 x = {x} - b 的形式（ 0≤b＜1 ）．

(1)、直接写出{x} 与 x ， x + 1的大小关系；
提示1：用“不完全归纳法”推导{x} 与 x ， x + 1的大小关系；

提示2：用“代数推理”的方法推导{x} 与 x ， x + 1的大小关系．

(2)、根据（1）中的结论解决下列问题：
①直接写出满足{3m + 7} = 4 的 m 取值范围；

②直接写出方程{3.5n - 2} = 2n + 1 的解．.

查看试题解析