上海市浦东新区第四教育署2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（　　）

A、 $2^{- 3}$ =﹣6 B、 $\sqrt[3]{- \frac{1}{8}} = - \frac{1}{2}$ C、 $\sqrt{4}$ =±2 D、2 $\sqrt{5}$ ×3 $\sqrt{2}$ =5 $\sqrt{10}$

查看试题解析
2. 下列各数： $\frac{π}{2}$ ，0， $\sqrt{9}$ ， $\frac{22}{7}$ ，0.3030030003， $1 - \sqrt{2}$ 中，无理数个数为（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列说法中错误的是（　　）

A、有两个角及它们的夹边对应相等的两个三角形全等 B、有两个角及其中一个角的对边对应相等的两个三角形全等 C、有两条边及它们的夹角对应相等的两个三角形全等 D、有两条边及其中一条边的对角对应相等的两个三角形全等

查看试题解析
4. 在直角坐标平面内，点P（﹣2，3）向下平移2个单位得到点Q，则点Q的坐标是（　　）

A、（﹣2，1） B、（﹣2，5） C、（0，3） D、（﹣4，3）

查看试题解析
5. 如图，BA//DE，∠B＝30°，∠D＝40°，则∠C的度数是（　　）

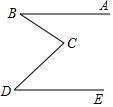A、10° B、35° C、70° D、80°

查看试题解析
6. 如图，已知OA＝OB，OC＝OD，AD和BC相交于点E，则图中共有全等三角形的对数（　　）

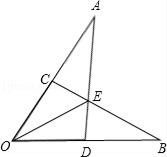A、2对 B、3对 C、4对 D、5对

查看试题解析

二、填空题

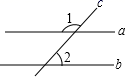
7. $\sqrt{25}$ 的平方根是；64的立方根是．

查看试题解析
8. 计算： $\sqrt{3}$ × $\sqrt{12}$ ＝．

查看试题解析
9. 计算： ${(\sqrt{3} - \sqrt{2})}^{^{2}}$ = .

查看试题解析
10. 把 $\frac{1}{\sqrt[5]{3^{4}}}$ 化成幂的形式：．

查看试题解析
11. 计算：（﹣ $\frac{3}{8}$ ）^﹣²＝．

查看试题解析
12. 我国最长的河流长江全长约为6300000米，将6300000用科学记数法表示应为．（保留3个有效数字）

查看试题解析
13. 一个等腰三角形两边的长分别为2m、5cm．则它的周长为cm．

查看试题解析
14. △ABC的三个内角的度数之比是1：2：3，若按角分类，则△ABC是三角形．

查看试题解析
15. 如图，直线a、b被直线c所截（即直线c与直线a、b都相交），且a//b，若∠1=118°，则∠2的度数=度．

查看试题解析
16. 如图，直线AB和CD交于O点，EO⊥CD，∠EOB=50°，则∠AOC= ．

查看试题解析
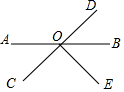17. 如图，在△ABC中，AB＝6，AC＝9，BO、CO分别是∠ABC、∠ACB的平分线，MN经过点O，且MN//BC，MN分别交AB、AC于点M、N，则△AMN的周长是．

查看试题解析
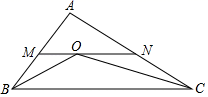18. 如图，在 $△ A B C$ 中，∠CAB＝65°，把 $△ A B C$ 绕着点A逆时针旋转到 $△ A B^{'} C^{'}$ ，联结CC'，并且使CC'//AB，那么旋转角的度数为度．

查看试题解析

三、解答题

19. 计算： $8^{\frac{2}{3}} - {(\sqrt{3})}^{2} \times \sqrt{6} \div \sqrt{2} + {(\frac{1}{\sqrt{3} - 1})}^{- 1}$ ．

查看试题解析
20. 利用幂的运算性质计算： ${(3^{\frac{7}{2}} \times 9^{- \frac{3}{4}})}^{\frac{1}{2}}$ ．

查看试题解析
21. 如图，已知∠COF+∠C＝180°，∠C＝∠B．说明AB//EF的理由．

查看试题解析
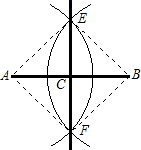
22. 阅读并填空：
如图：根据六年级第二学期学过的用直尺、圆规作线段中点的方法，画出了线段AB的中点C，请说明这种方法正确的理由．

解：连接AE、BE、AF、BF．

在△AEF和△BEF中，

EF＝EF（），

＝（画弧时所取的半径相等），

＝（画弧时所取的半径相等）．

所以△AEF≌△BEF （）．

所以∠AEF＝∠BEF （）．

又AE＝BE，

所以AC＝BC （）．

即点C是线段AB的中点．

查看试题解析
23. 在直角坐标平面内，点A₁、B₁、C₁的坐标如图所示．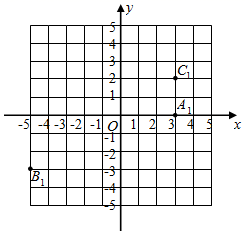

(1)、请写出点A₁、B₁、C₁的坐标：
点A₁的坐标是；

点B₁的坐标是；

点C₁的坐标是．

(2)、将点A₁绕原点逆时针旋转90°得到点A，则点A的坐标是．

(3)、若点B₁与点B关于原点对称，则点B的坐标是．

(4)、将C₁沿x轴翻折得到点C，则点C的坐标是．

(5)、分别联结AB、BC、AC，得到△ABC，则△ABC的面积是．

查看试题解析
24. 如图，已知在等腰三角形ABC中，AB＝AC，∠BAC＝80°，AD⊥BC，AD＝AB，联结BD并延长，交AC的延长线于点E，求∠E的度数．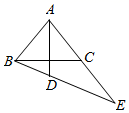

查看试题解析
25. 如图，已知点C是线段AB上一点，∠DCE＝∠A＝∠B，CD＝CE．

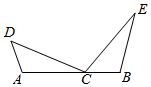(1)、说明△ACD与△BEC全等的理由；

(2)、说明AB＝AD+BE的理由．

查看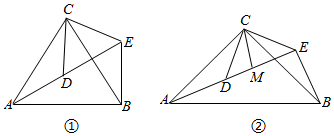试题解析
26.
如图①，△ACB和△DCE都是等边三角形，点A、D、E在同一条直线上，联结BE．

(1)、说明△CAD和△CBE全等的理由．

(2)、填空：∠AEB的度数为；线段AD和BE的数量关系是：．（直接写出答案）

(3)、如图②，△ACB和△DCE都是等腰直角三角形，∠ACB＝∠DCE＝90°，点A、D、E在同一条直线上，CM为△DCE中DE边上的高，联结BE．则∠AEB的度数为；线段CM、AE、BE之间的数量关系是：．（直接写出答案）

查看试题解析