内蒙古自治区乌海市海勃湾区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 下列实数中,无理数的个数是( )
①0. ;② ;③ ;④π;⑤ ;⑥6.18118111811118……
A、1 个 B、2 个 C、3 个 D、4 个2. 在同一平面内,两条直线的位置关系是( )A、平行和垂直 B、平行和相交 C、垂直和相交 D、平行、垂直和相交3. 如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( ) A、80° B、90° C、100° D、102°4. 已知 a<b , 下列式子成立的是( )A、﹣a>b B、c﹣4a>c﹣4b C、|a| |b| D、ab<5. 如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示 ﹣1的点是( )
A、80° B、90° C、100° D、102°4. 已知 a<b , 下列式子成立的是( )A、﹣a>b B、c﹣4a>c﹣4b C、|a| |b| D、ab<5. 如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示 ﹣1的点是( )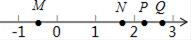 A、点M B、点N C、点P D、点Q6. 下列说法正确的是( )A、1的平方根是1 B、 的算术平方根是9 C、(−6 没有平方根 D、立方根等于本身的数是0和±17. 以下是四位同学在钝角三角形 ABC 中画 AC 边上的高,其中正确的是( )A、
A、点M B、点N C、点P D、点Q6. 下列说法正确的是( )A、1的平方根是1 B、 的算术平方根是9 C、(−6 没有平方根 D、立方根等于本身的数是0和±17. 以下是四位同学在钝角三角形 ABC 中画 AC 边上的高,其中正确的是( )A、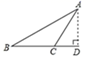 B、
B、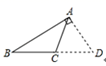 C、
C、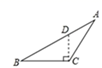 D、
D、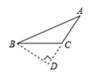 8. 去年我市有 3500 名考生参加中考,为了了解这些考生的数学成绩,从中抽取 1000 名考生的数学成绩进行统计分析,在这个调查中,下列说法:①这 3500 名考生的数学中考成绩的全体是总体;②每个考生是个体;③1000 名考生是总体的一个样本;④样本容量是 1000. 其中正确的有( )A、4 个 B、3 个 C、2 个 D、1 个9. 以方程组 的解为坐标的点(x , y)在平面直角坐标系中的位置是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m , 则两条小路的总面积是( )m2
8. 去年我市有 3500 名考生参加中考,为了了解这些考生的数学成绩,从中抽取 1000 名考生的数学成绩进行统计分析,在这个调查中,下列说法:①这 3500 名考生的数学中考成绩的全体是总体;②每个考生是个体;③1000 名考生是总体的一个样本;④样本容量是 1000. 其中正确的有( )A、4 个 B、3 个 C、2 个 D、1 个9. 以方程组 的解为坐标的点(x , y)在平面直角坐标系中的位置是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m , 则两条小路的总面积是( )m2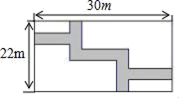 A、108 B、104 C、100 D、9811. 下列语句中,为真命题的是( )A、过一点有且只有一条直线与已知直线平行 B、有理数与数轴上的点一一对应 C、互为邻补角的角的平分线所在的两条直线互相垂直 D、垂直于同一条直线的两条直线平行12. 若关于 x 的不等式组 恰好只有 2 个整数解,则所有满足条件的整数 a 的值之和是( )A、3 B、4 C、6 D、1
A、108 B、104 C、100 D、9811. 下列语句中,为真命题的是( )A、过一点有且只有一条直线与已知直线平行 B、有理数与数轴上的点一一对应 C、互为邻补角的角的平分线所在的两条直线互相垂直 D、垂直于同一条直线的两条直线平行12. 若关于 x 的不等式组 恰好只有 2 个整数解,则所有满足条件的整数 a 的值之和是( )A、3 B、4 C、6 D、1二、填空题
-
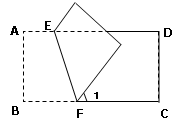
13. 若 2a-1和a-1是一个正数?的两个平方根,则?= .14. 一个两位数,个位数字与十位数字之和为 10,交换这两个数字的位置所得的两位数比原数大 36,则这个两位数是 .15. 如图,把长方形ABCD沿EF对折,若∠1=500 , 则∠AEF的度数等于.
 16. 已知点M(3a-9,1-a),将M点向左平移3个单位长度后落在y轴上,则点M的坐标为 .17. 已知(2a+b 与 互为相反数,则 = .18. 如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是 .19. 将命题“同角的余角相等”,改写成“如果…,那么…”的形式.20. 观察下列各式: =2 ; =3 ; =4 ,……请你将发现的规律用含自然数n(n≥1)的等式表示出来 .
16. 已知点M(3a-9,1-a),将M点向左平移3个单位长度后落在y轴上,则点M的坐标为 .17. 已知(2a+b 与 互为相反数,则 = .18. 如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是 .19. 将命题“同角的余角相等”,改写成“如果…,那么…”的形式.20. 观察下列各式: =2 ; =3 ; =4 ,……请你将发现的规律用含自然数n(n≥1)的等式表示出来 .三、解答题
-
21. 某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成如下统计图表进行分析.
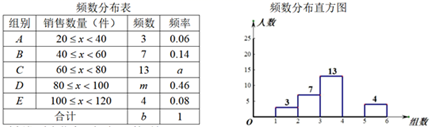
请根据上述统计图表,解答下列问题:
(1)、表中a= , b=;(2)、补全频数分布直方图;(3)、如果该季度销量不低于80件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.22. 解方程组 时,一学生把 c 看错而得到 ,而正确的解是 ,求a , b , c 的值.23. 如图,在数轴上点A、B、C分别表示-1、-2x+3、x+1,且点A在点B的左侧,点C在点B的右侧.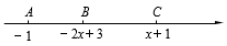 (1)、求x的取值范围;(2)、当AB=2BC时,x的值为.24. 如图所示,已知点A(2,1),B(8,2),C(6,3).
(1)、求x的取值范围;(2)、当AB=2BC时,x的值为.24. 如图所示,已知点A(2,1),B(8,2),C(6,3).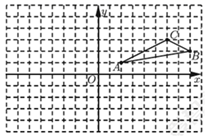 (1)、若将△ABC向下平移 5个单位长度,再向左平移 9个单位长度,得到△A′B′C′,画出平移后图形并写出各顶点的坐标.(2)、求△ABC的面积.25. 目前节能灯已基本普及,节能还环保,销量非常好,某商场计划购进甲、乙两种型号节能灯共1200只,这两种节能灯的进价、售价如表所示:
(1)、若将△ABC向下平移 5个单位长度,再向左平移 9个单位长度,得到△A′B′C′,画出平移后图形并写出各顶点的坐标.(2)、求△ABC的面积.25. 目前节能灯已基本普及,节能还环保,销量非常好,某商场计划购进甲、乙两种型号节能灯共1200只,这两种节能灯的进价、售价如表所示:进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、商场应如何进货,使进货款恰好为46000元?(2)、若商场销售完节能灯后获利不超过进货价的30%,至少购进甲种型号节能灯多少只?26. 如图1,直线MN与直线AB、CD分别交于点E、F , ∠1与∠2互补.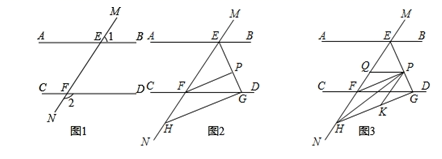 (1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P , EP与CD交于点G , 点H是MN上一点,且GH⊥EG , 求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH , K是GH上一点使∠PHK=∠HPK , 作PQ平分∠EPK , 求∠HPQ的度数.
(1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P , EP与CD交于点G , 点H是MN上一点,且GH⊥EG , 求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH , K是GH上一点使∠PHK=∠HPK , 作PQ平分∠EPK , 求∠HPQ的度数.