北京市丰台区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 4的平方根是( )A、 B、 C、2 D、2. 不等式x-1<0的解集在数轴上表示正确的是( )A、
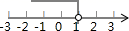 B、
B、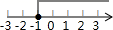 C、
C、 D、
D、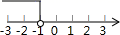 3. 二元一次方程组 的解是( )A、 B、 C、 D、4. 适宜表示一组数据的变化趋势的统计图是( )A、条形图 B、扇形图 C、折线图 D、直方图5. 下列实数中的无理数是( )A、 B、 C、 D、06. 如图,由 可以得到( )
3. 二元一次方程组 的解是( )A、 B、 C、 D、4. 适宜表示一组数据的变化趋势的统计图是( )A、条形图 B、扇形图 C、折线图 D、直方图5. 下列实数中的无理数是( )A、 B、 C、 D、06. 如图,由 可以得到( )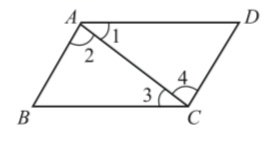 A、 B、 C、 D、7. 如图,数轴上与 对应的点是( )
A、 B、 C、 D、7. 如图,数轴上与 对应的点是( )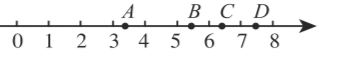 A、点 B、点 C、点 D、点8. 下列命题正确的是( )A、两个相等的角一定是对顶角 B、两条直线被第三条直线所截,同旁内角互补 C、两个锐角的和是锐角 D、连接直线外一点与直线上各点的所有线段中,垂线段最短9. 下图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,当表示地安门的点的坐标为 ,表示广安门的点的坐标为 时,那么表示左安门的点的坐标为( )
A、点 B、点 C、点 D、点8. 下列命题正确的是( )A、两个相等的角一定是对顶角 B、两条直线被第三条直线所截,同旁内角互补 C、两个锐角的和是锐角 D、连接直线外一点与直线上各点的所有线段中,垂线段最短9. 下图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,当表示地安门的点的坐标为 ,表示广安门的点的坐标为 时,那么表示左安门的点的坐标为( )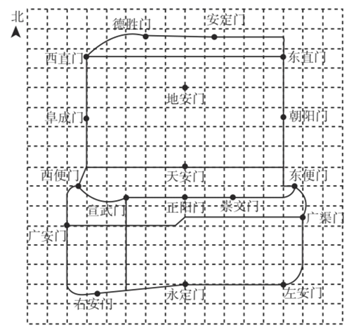 A、 B、 C、 D、10. 小明统计了同学们5月份平均每天观看北京市“空中课堂”的时间,并绘制了统计图,如图所示下面有四个推断
A、 B、 C、 D、10. 小明统计了同学们5月份平均每天观看北京市“空中课堂”的时间,并绘制了统计图,如图所示下面有四个推断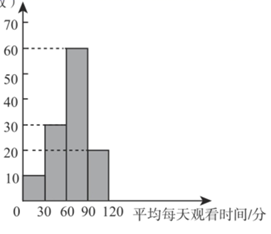
①此次调查中,小明一共调查了100名学生
②此次调查中,平均每天观看时间不足30分钟的人数占总人数的10%
③此次调查中,平均每天观看时间超过60分钟的人数超过调查总人数的一半
④此次调查中,平均每天观看时间不足60分钟的人数少于平均每天观看时间在60-90分钟的人数
所有合理推断的序号是( )
A、①② B、①④ C、③④ D、②③④二、填空题
-
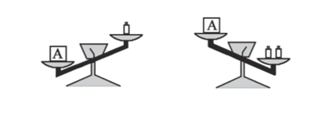
11. 写出方程 的一个解 .12. 如果 ,那么x= .13. 在平面直角坐标系中,已知点 ,点 ,那么 .14. 如图,天平左盘中物体A的质量为x克,天平右盘中每个砝码的质量都是5克那么x的取值范围为 .
 15. 如图,木工师傅可以用角尺画平行线,能解释这一实际应用的数学知识是 .
15. 如图,木工师傅可以用角尺画平行线,能解释这一实际应用的数学知识是 .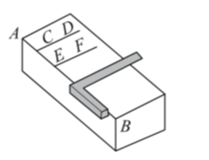 16. 我国古代数学著作《九章算术》中记载:“今有大器五小器一容三斛,大器一小器五容二斛.问大小器各容几何.”其大意为:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,音hu , 是古代的一种容量单位).1个大桶加上5个小桶可以盛酒2斛,问1个大桶、一个小桶分别可以盛酒多少斛?若设1个大桶可以盛酒x斛,1个小桶可以盛酒y斛,根据题意,可列方程组为.17. 一副三角尺按如图所示的位置摆放,那么 .
16. 我国古代数学著作《九章算术》中记载:“今有大器五小器一容三斛,大器一小器五容二斛.问大小器各容几何.”其大意为:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,音hu , 是古代的一种容量单位).1个大桶加上5个小桶可以盛酒2斛,问1个大桶、一个小桶分别可以盛酒多少斛?若设1个大桶可以盛酒x斛,1个小桶可以盛酒y斛,根据题意,可列方程组为.17. 一副三角尺按如图所示的位置摆放,那么 .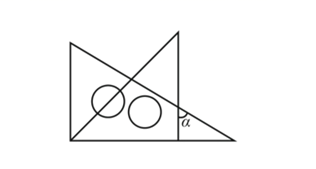 18. 如图,在平面直角坐标系 中,三角形 可以看作是三角形 经过平移得到的,写出一种由三角形 得到三角形 的过程: .
18. 如图,在平面直角坐标系 中,三角形 可以看作是三角形 经过平移得到的,写出一种由三角形 得到三角形 的过程: .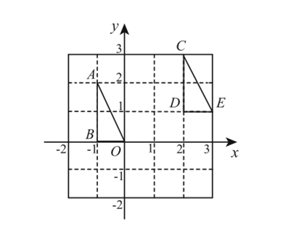
三、解答题
-
19. 计算:20. 解方程组:21. 解不等式组 并写出它的所有正整数解22. 画一条线段的垂线,就是画它所在直线的垂线.如图,请你过点P画出线段 的垂线,垂足分别为点 .
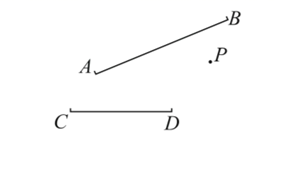 23. 完成下面的证明
23. 完成下面的证明如图,三角形 .D是边 延长线上一点,过点C作射线 ,
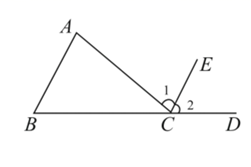
求证:
证明:∵
∴//()
∴ ()
∵ ()
∴
24. 列方程或方程组解应用题病毒无情,人间有爱.全国医务人员在党中央的号召下,面对疫情,主动请缨,前往湖北支援.北京市属医院首批援助队伍除领队外共135名医务人员,负责5个针对普通感染者的病区和1个针对危重感染者的病区.如果知道针对普通感染者的每个病区和针对危重感染者的每个病区配备医务人员的比例为1:4.请你计算北京市属医院首批援助队伍中负责普通感染者病区和负责危重感染者病区的医务人员各有多少人.
25. 某校七~九年级共有400名学生,学校团委准备调查他们对垃圾分类的了解程度.(1)、下面有三种选取调查对象的方式:①调查七~九年级部分女生
②调查七年级某个班的学生
③随机调查七~九年级每个班一定数量的学生.
你认为最合理的一种方式是 . (直接填写序号);
(2)、学校团委采用了最合理的调査方式,并用收集到的数据绘制出两幅统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;
图①

图②
(3)、根据此次调查结果,估计该校七~九年级约有名学生对垃圾分类比较了解;(4)、根据此次调查结果,请你为学校团委开展垃圾分类主题教育活动提出合理化建议26. 在平面直角坐标系 中,对于任意一点 ,定义点P的“差距离” 为: .例如:已知点 ,则 .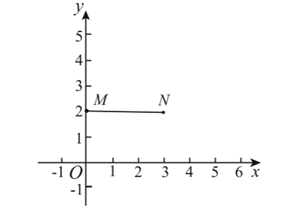
解决下列问题:
(1)、已知点 ,则 .(2)、如图,点 是线段 上的一动点,①若 ,求点 的坐标;
②线段MN向右平移m个单位 ,点Q的对应点为 ,如果 ,求m的取值范围;
③线段MN向右平移a个单位 ,向上平移b个单位 后得到线段 .若线段 上“差距离”为1的点恰有两个,直接写出 的取值范围