北京市朝阳区2019-2020学年七年级下学期数学期末试卷(选用)
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 下列各图中,∠1和∠2是对顶角的是( )A、
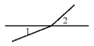 B、
B、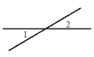 C、
C、 D、
D、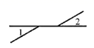 2. 以下调查中,适宜抽样调查的是( )A、了解某班学生的身高情况 B、调查某批次汽车的抗撞击能力 C、掌握疫情期间某班学生体温情况 D、选出某校短跑最快的学生参加全市比赛3. 下列说法错误的是( )A、3的平方根是 B、﹣1的立方根是﹣1 C、0.1是0.01的一个平方根 D、算术平方根是本身的数只有0和14. 在平面直角坐标系中,下列各点位于第二象限的是( )A、 B、 C、 D、5. 若 是关于 和 的二元一次方程 的解,则 的值等于( )A、3 B、1 C、 D、6. 如图,点D , E , F分别是三角形ABC的边BC , CA , AB上的点,DE∥BA , DF∥CA . 图中与∠A不一定相等的角是( )
2. 以下调查中,适宜抽样调查的是( )A、了解某班学生的身高情况 B、调查某批次汽车的抗撞击能力 C、掌握疫情期间某班学生体温情况 D、选出某校短跑最快的学生参加全市比赛3. 下列说法错误的是( )A、3的平方根是 B、﹣1的立方根是﹣1 C、0.1是0.01的一个平方根 D、算术平方根是本身的数只有0和14. 在平面直角坐标系中,下列各点位于第二象限的是( )A、 B、 C、 D、5. 若 是关于 和 的二元一次方程 的解,则 的值等于( )A、3 B、1 C、 D、6. 如图,点D , E , F分别是三角形ABC的边BC , CA , AB上的点,DE∥BA , DF∥CA . 图中与∠A不一定相等的角是( )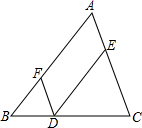 A、∠BFD B、∠CED C、∠AED D、∠EDF7. 若a>b,则下列不等式成立的是( )A、a+2<b+2 B、a﹣2<b﹣2 C、3a<3b D、﹣ <﹣8. 小明用计算器求了一些正数的平方,记录如下表.
A、∠BFD B、∠CED C、∠AED D、∠EDF7. 若a>b,则下列不等式成立的是( )A、a+2<b+2 B、a﹣2<b﹣2 C、3a<3b D、﹣ <﹣8. 小明用计算器求了一些正数的平方,记录如下表.x
15
15.1
15.2
15.3
15.4
15.5
15.6
15.7
15.8
15.9
16
225
228.01
231.04
234.09
237.16
240.25
243.36
246.49
249.64
252.81
256
下面有四个推断:
① =1.51
②一定有3个整数的算术平方根在15.5~15.6之间
③对于小于15的两个正数,若它们的差等于0.1,则它们的平方的差小于3.01
④16.22比16.12大3.23
所有合理推断的序号是( )
A、①② B、③④ C、①②④ D、①②③④二、填空题
-
9. π的相反数是.10. 把方程2x-y=3用含x的式子表示y的形式是.11. 某个关于x的不等式的解集在数轴上的表示如图所示,这个不等式的解集是 .
 12. 如图,在一块长方形草地上原有一条等宽的笔直小路,现在要把这条小路改为同样宽度的等宽弯曲小路,则改造后小路的长度 , 草地部分的面积 . (填“变大”,“不变”或“变小”)
12. 如图,在一块长方形草地上原有一条等宽的笔直小路,现在要把这条小路改为同样宽度的等宽弯曲小路,则改造后小路的长度 , 草地部分的面积 . (填“变大”,“不变”或“变小”) 13. 如图,AB∥CD , CE平分∠ACD , 若∠A=110°,则∠AEC=°.
13. 如图,AB∥CD , CE平分∠ACD , 若∠A=110°,则∠AEC=°.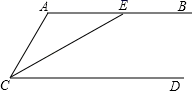 14. 在平面直角坐标系xOy中,点M的坐标为(0,2),若三角形MOP的面积为1,写出一个满足条件的点P的坐标: .15. 可以用一个m的值说明命题“如果m能被2整除,那么它也能被4整除”是假命题,这个值可以是m= .16. A(a , 0),B(3,4)是平面直角坐标系中的两点,线段AB长度的最小值为 .17.(1)、完成框图中解方程组的过程:
14. 在平面直角坐标系xOy中,点M的坐标为(0,2),若三角形MOP的面积为1,写出一个满足条件的点P的坐标: .15. 可以用一个m的值说明命题“如果m能被2整除,那么它也能被4整除”是假命题,这个值可以是m= .16. A(a , 0),B(3,4)是平面直角坐标系中的两点,线段AB长度的最小值为 .17.(1)、完成框图中解方程组的过程: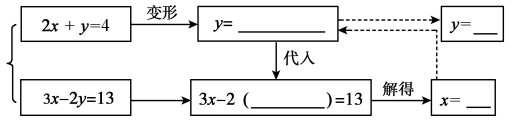 (2)、上面框图所表示的解方程组的方法是: .
(2)、上面框图所表示的解方程组的方法是: .三、解答题
-
18. 计算: ﹣ + ( +1).19. 解方程组 .20. 解不等式 >x﹣1,并写出它的所有正整数解.21. 完成下面的证明.
已知:如图,∠1+∠2=180°,∠3+∠4=180°.
求证:AB∥EF .
证明:∵∠1+∠2=180°,
∴AB∥().
∵∠3+∠4=180°,
∴∥ .
∴AB∥EF().
 22. 列方程组解应用题:
22. 列方程组解应用题:2020年5月1日,新修订的《北京市生活垃圾管理条例》正式实施,生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类.北京市现有生活垃圾处理设施中的焚烧设施和生化设施共34座,总处理能力达到约24550吨/日,其中每一座焚烧设施处理能力约为1500吨/日,每一座生化设施处理能力约为350吨/日.则北京市现有生活垃圾处理设施中的焚烧设施和生化设施各有多少座?
23. 在近几年的两会中,有多位委员不断提出应在中小学开展编程教育,2019年3月教育部公布的《2019年教育信息化和网络安全工作要点》中也提出将推广编程教育.某学校的编程课上,一位同学设计了一个运算程序,如图所示.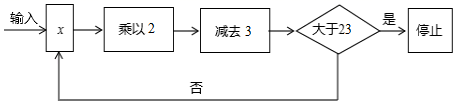
按上述程序进行运算,程序运行到“判断结果是否大于23”为一次运行.
(1)、若x=5,直接写出该程序需要运行多少次才停止;(2)、若该程序只运行了2次就停止了,求x的取值范围.24. 线段AB与线段CD互相平行,P是平面内的一点,且点P不在直线AB , CD上,连接PA , PD , 射线AM , DN分别是∠BAP和∠CDP的平分线.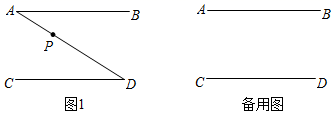 (1)、若点P在线段AD上,如图1,
(1)、若点P在线段AD上,如图1,①依题意补全图1;
②判断AM与DN的位置关系,并证明;
(2)、是否存在点P , 使AM⊥DN?若存在,直接写出点P的位置;若不存在,说明理由.25. 我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案,众人十分惊奇,忙问计算的奥妙.你知道他是怎样迅速准确地计算出结果的吗?下面是小超的探究过程,请补充完整:
(1)、求 ;①由103=1000,1003=1 000 000,可以确定 是位数;
②由59319的个位上的数是9,可以确定 的个位上的数是;
③如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定 的十位上的数是;
由此求得 = .
(2)、已知103823也是一个整数的立方,用类似的方法可以求得 = .26. 如图,在平面直角坐标系xOy中,A(﹣5,0),B(﹣1,0),M(0,5),N(5,0),连接MN , 以AB为边在x轴上方作正方形ABCD .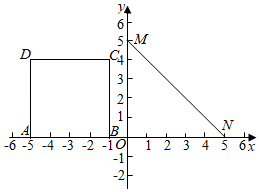 (1)、直接写出C , D两点的坐标;(2)、将正方形ABCD向右平移t个单位长度,得到正方形A′B′C′D′.
(1)、直接写出C , D两点的坐标;(2)、将正方形ABCD向右平移t个单位长度,得到正方形A′B′C′D′.①当点C′落在线段MN上时,结合图形直接写出此时t的值;
②横、纵坐标都是整数的点叫做整点,记正方形A′B′C′D′和三角形OMN重叠的区域(不含边界)为W , 若区域W内恰有3个整点,直接写出t的取值范围.