广东省佛山市三水区2019-2020学年七年级下学期数学期末试卷
试卷更新日期：2020-09-16 类型：期末考试
一、单选题
-
1. 下列运算正确的是（ ）A、a+b=ab B、（x+1）2 =x2+1 C、a10÷ a5=a2 D、（﹣a3）2=a62. 某种细胞直径是0.00000095米，将0.00000095用科学记数法表示为（ ）A、9.5×10﹣7 B、9.5×10﹣8 C、0.95×10﹣6 D、95×10﹣83. 以每组数为线段的长度，可以构成三角形三边的是（ ）A、5，6，10 B、5，6，11 C、3，4，8 D、4，4，84. 下列事件中，是必然事件的是（ ）A、内错角相等 B、掷两枚硬币，必有一个正面朝上，一个反面朝上 C、13人中至少有两个人的生肖相同 D、打开电视，一定能看到三水新闻5. 如果∠A=50°，那么∠A的余角是（ ）A、30° B、40° C、90° D、130°6. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
7. 如图，把一副三角板放在桌面上，当AB∥DC时，∠CAE等于（ ）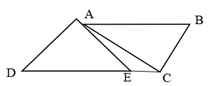
A、10° B、15° C、20° D、25°8. 一个长方体的长、宽、高分别是3m－4，2m和m，则它的体积是（ ）A、3m3－4m2 B、3m2－4m3 C、6m3－8m2 D、6m2－8m39. 为了应用平方差公式计算（a﹣b+c）（a+b﹣c），必须先适当变形，下列变形中，正确的是（ ）A、[(a+c)﹣b] [(a﹣c)+b] B、[(a﹣b)+c][(a+b)﹣c] C、[a﹣(b+c)] [a+(b﹣c)] D、[a﹣(b﹣c)] [a+(b﹣c)]10. 如图所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家，其中x表示时间，y表示张强离家的距离．根据图象提供的信息，以下四个说法错误的有（ ）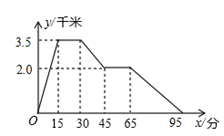
①体育场离张强家3.5千米 ②张强在体育场锻炼了15分钟
③体育场离早餐店1.5千米 ④张强从早餐店回家的平均速度是3千米/小时
A、1个 B、2个 C、3个 D、4个二、填空题
-
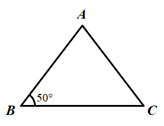
11. 计算：（﹣a）2•a3= ．12. 若ax=2，ay=3，则ax-y= ．13. 如图所示，在△ABC中，AB＝AC ， ∠B＝50°，则∠A＝ ．
14. 有5张纸签，分别标有数字2，3，4，5，6，从中随机抽出一张，则抽出标有数字为偶数的概率为 ．15. 已知等腰三角形的两边长分别为3,6，则这个等腰三角形的周长为.16. 三角形的底边长为8，高是x，那么三角形的面积y与高x之间的关系式是 ．17. 如图，已知∠ACB=90°，BC=6，AC=8，AB=10，点D在线段AB上运动，线段CD的最短距离是 ．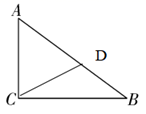
三、解答题
-
18. ﹣32+50﹣( )﹣2+(﹣1)202019. 先化简再求值：[（x﹣y）2﹣（y﹣x）（y+x）]÷2x，其中x=2021，y=1．20. 元旦期间，某超市开展有奖促销活动，凡在超市购物的顾客均有转动圆盘的机会（如图），如果规定当圆盘停下来时指针指向8就中一等奖，指向2或6就中二等奖，指向1或3或5就中纪念奖，指向其余数字不中奖．
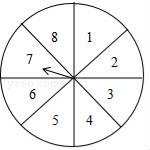(1)、转动转盘中奖的概率是多少？(2)、元旦期间有1000人参与这项活动，估计获得一等奖的人数是多少？21. 如图，AB＝CD，AF＝CE，∠A＝∠C，那么BE=DF吗？请说明理由．
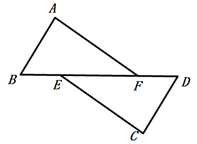22. 三水区响应“绿色环保”号召，鼓励市民节约用电，对电费采用分段收费标准，若某户居民每月应交电费y(元)与用电量x(度)之间关系的图象如图所示：
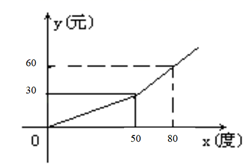(1)、当用电量不超过50度时，每度收费多少元？超过50度时，超过的部分每度收费多少元？(2)、若某户居民某月交电费120元，该户居民用电多少度？23. 如图，在△ABC中，∠C=60°，∠A=40°．用尺规作图作边AB的垂直平分线，交AC于点D，交AB于点E（要求：不写作法，保留作图痕迹）.
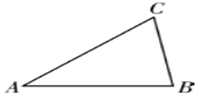24. 对于一个平面图形，通过两种不同的方法计算它的面积，可以得到一个关于整式乘法的数学等式，例如图1可以得到完全平方公式(a+b)2=a2+2ab+b2 ， 请利用这一方法解决下列问题：
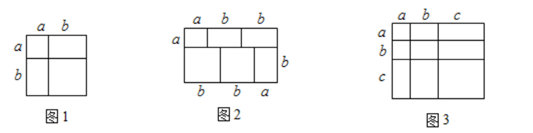(1)、观察图2，写出所表示的数学等式：= ．
(2)、观察图3，写出所表示的数学等式：= ．
(3)、已知（2）的等式中的三个字母可以取任何数，若a=7x－5，b=﹣4x+2，c=﹣3x+4，且a2+b2+c2=37．请利用（2）中的结论求ab+bc+ac的值．25. 如图（1），AB=7cm，AC⊥AB，BD⊥AB，AC=5cm．点P在线段AB上以2cm/s的速度由点A向点B运动，同时，点Q在射线BD上由点B向点D运动．它们运动的时间为t（s），当点P到达点B时，点Q也停止运动．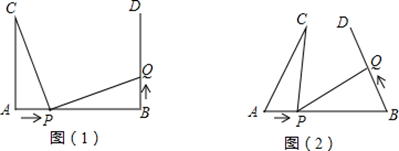
(1)、若点Q的运动速度与点P的运动速度相等，当t=1s时，△ACP与△BPQ全等，此时PC⊥PQ吗？请说明理由．(2)、将图(1)中的“AC⊥AB，BD⊥AB”为改“∠CAB=∠DBA=60°”后得到如图（2），其他条件不变．设点Q的运动速度为xcm/s．当点P、Q运动到某处时，有△ACP与△BPQ全等，求出相应的x、t的值．(3)、在（2）成立的条件下且P、Q两点的运动速度相同时，∠CPQ= ． （直接写出结果）