广东省东莞市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 在 中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 下列等式成立的是( )A、 B、 C、 D、3. 下列式子是二元一次方程的是( )A、 B、 C、 D、4. 如图,直线a、b被直线c所截,若 ,则下列错误的是( )
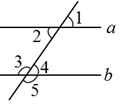 A、 B、 C、 D、5. 为了了解某校学生早晨就餐的情况,四位同学分别作了不同的调查:小华分别向701班、801班、901班的全体同学作了调查;小明向701班、702班、703班3个班的全体同学作了调查;小芳抽取8年级三个班的全体同学作了调查;小珍向9年级的全体同学作了调查,其中抽样调查较科学的是( )A、小华 B、小明 C、小芳 D、小珍6. 点P(2,-3)到x轴的距离等于( )A、-2 B、2 C、-3 D、37. 若 ,则下列各式一定成立的是( )A、 B、 C、 D、8. 不等式组 的解集在数轴上表示为A、
A、 B、 C、 D、5. 为了了解某校学生早晨就餐的情况,四位同学分别作了不同的调查:小华分别向701班、801班、901班的全体同学作了调查;小明向701班、702班、703班3个班的全体同学作了调查;小芳抽取8年级三个班的全体同学作了调查;小珍向9年级的全体同学作了调查,其中抽样调查较科学的是( )A、小华 B、小明 C、小芳 D、小珍6. 点P(2,-3)到x轴的距离等于( )A、-2 B、2 C、-3 D、37. 若 ,则下列各式一定成立的是( )A、 B、 C、 D、8. 不等式组 的解集在数轴上表示为A、 B、
B、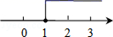 C、
C、 D、
D、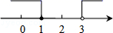 9. 二元一次方程组 的解是( )A、 B、 C、 D、10. 如图,轮船航行到B处观测小岛A的方向是北偏西32°,那么小岛A观测到轮船B的方向是( )
9. 二元一次方程组 的解是( )A、 B、 C、 D、10. 如图,轮船航行到B处观测小岛A的方向是北偏西32°,那么小岛A观测到轮船B的方向是( )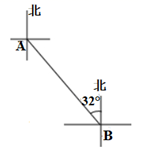 A、南偏西32 ° B、南偏东32° C、南偏西58° D、南偏东58°
A、南偏西32 ° B、南偏东32° C、南偏西58° D、南偏东58°二、填空题
-
11. 所在的象限是第象限.12. 49的平方根是 .13. 为了解一批灯管的使用寿命,适合采用的调查方式是(填“普查”或“抽样调查”)14. 已知 是方程 的解,则k的值为 .15. 若式子 的值比式子 的值大,则x的取值范围是 .16. 如图,已知 ,直线 过点O, 且 ,那么 .
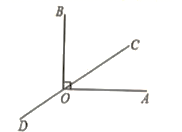 17. 有一个数值转换器,原理如下:当输入x为4时,输出的y的值是 .
17. 有一个数值转换器,原理如下:当输入x为4时,输出的y的值是 .
三、解答题
-
18. 计算: .19. 解不等式组 并将其正整数解写出来.20. 已知摄氏温度 与华氏温度 之间存在下表关系:
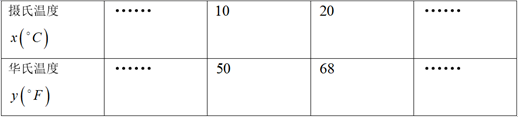 (1)、华氏温度 与摄氏温度 之间满足一次函数关系,请求出y关于x的函数解析式;(2)、求华氏温度是 时,摄氏温度的值.21. 如图,平面直角坐标系中, 的顶点坐标为: .将 向右平移6个单位长度,再向上平移3个单位长度,得到对应的 .
(1)、华氏温度 与摄氏温度 之间满足一次函数关系,请求出y关于x的函数解析式;(2)、求华氏温度是 时,摄氏温度的值.21. 如图,平面直角坐标系中, 的顶点坐标为: .将 向右平移6个单位长度,再向上平移3个单位长度,得到对应的 .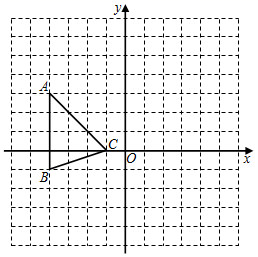 (1)、画出 ,并写出 的坐标;(2)、直接写出 的面积.22. 在等式 中,当 时, ;当 时, .(1)、求 的值;(2)、求当 时y的值.23. 某中学为了提高学生的综合素质,成立了以下社团:A(机器人),B(围棋),C(羽毛球),D(电影配音),每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成两幅不完整的统计图(如图).根据上述信息,解答下列问题:
(1)、画出 ,并写出 的坐标;(2)、直接写出 的面积.22. 在等式 中,当 时, ;当 时, .(1)、求 的值;(2)、求当 时y的值.23. 某中学为了提高学生的综合素质,成立了以下社团:A(机器人),B(围棋),C(羽毛球),D(电影配音),每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成两幅不完整的统计图(如图).根据上述信息,解答下列问题:
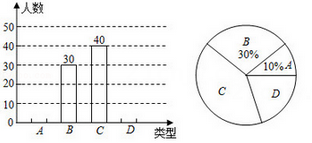
(1)、这次一共调查了多少人?(2)、求“A”在扇形统计图中所占圆心角的度数;(3)、请将条形统计图补充完整.