北京市海淀区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 如图所示,∠2 和∠1 是对顶角的是( )A、
 B、
B、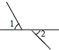 C、
C、 D、
D、 2. 4的平方根是( )A、±16 B、 C、 D、3. 已知 ,下列不等式中,变形正确的是( ).A、 B、 C、 D、4. 在平面直角坐标系中,如果点 在第三象限,那么m的取值范围为( )A、 B、 C、 D、5. 下列调查方式,你认为最合适的是( )A、了解某地区饮用水矿物质含量的情况,采用抽样调查方式 B、旅客上飞机前的安检,采用抽样调查方式 C、调查某种品牌笔芯的使用寿命,采用全面调查方式 D、调查浙江卫视《奔跑吧,兄弟》节目的收视率,采用全面调查方式6. 如图,将含30°角的直角三角板的直角顶点放在直尺的一边上,已知∠1=35°,则∠2的度数是( ).
2. 4的平方根是( )A、±16 B、 C、 D、3. 已知 ,下列不等式中,变形正确的是( ).A、 B、 C、 D、4. 在平面直角坐标系中,如果点 在第三象限,那么m的取值范围为( )A、 B、 C、 D、5. 下列调查方式,你认为最合适的是( )A、了解某地区饮用水矿物质含量的情况,采用抽样调查方式 B、旅客上飞机前的安检,采用抽样调查方式 C、调查某种品牌笔芯的使用寿命,采用全面调查方式 D、调查浙江卫视《奔跑吧,兄弟》节目的收视率,采用全面调查方式6. 如图,将含30°角的直角三角板的直角顶点放在直尺的一边上,已知∠1=35°,则∠2的度数是( ). A、55° B、45° C、35° D、65°7. 下列命题中,是假命题的是( ).A、在同一平面内,过一点有且只有一条直线与已知直线垂直. B、同旁内角互补,两直线平行. C、如果两条直线都与第三条直线平行,那么这两条直线也互相平行. D、两条直线被第三条直线所截,同位角相等.8. 如图,O为直线AB上一点,OE平分∠BOC,OD⊥OE于点O,若∠BOC=80°,则∠AOD的度数是( )
A、55° B、45° C、35° D、65°7. 下列命题中,是假命题的是( ).A、在同一平面内,过一点有且只有一条直线与已知直线垂直. B、同旁内角互补,两直线平行. C、如果两条直线都与第三条直线平行,那么这两条直线也互相平行. D、两条直线被第三条直线所截,同位角相等.8. 如图,O为直线AB上一点,OE平分∠BOC,OD⊥OE于点O,若∠BOC=80°,则∠AOD的度数是( ) A、35° B、40° C、50° D、70°9. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
A、35° B、40° C、50° D、70°9. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( ) A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x , x的二元一次方程组 的解,那么这个点是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x , x的二元一次方程组 的解,那么这个点是( )
 A、M B、N C、E D、F
A、M B、N C、E D、F二、填空题
-
11. 用不等式表示:a与2的差小于 -112. 把无理数 , , ,- 表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是 .
 13. 若 ,则 .14. 写出二元一次方程 的一个非负整数解 .15. 如图,写出能判定AB∥CD的一对角的数量关系:.
13. 若 ,则 .14. 写出二元一次方程 的一个非负整数解 .15. 如图,写出能判定AB∥CD的一对角的数量关系:.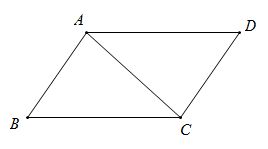 16. 在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x, )的纵坐标满足 ,那么称点Q为点P的“关联点”.请写出点(3,5)的“关联点”的坐标;如果点P(x,y)的关联点Q坐标为(-2,3),则点P的坐标为 .
16. 在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x, )的纵坐标满足 ,那么称点Q为点P的“关联点”.请写出点(3,5)的“关联点”的坐标;如果点P(x,y)的关联点Q坐标为(-2,3),则点P的坐标为 .三、解答题
-
17. 计算 .18. 解二元一次方程组19. 解不等式组 ,并把它的解集在数轴上表示出来.
 20. 按要求完成下列证明:
20. 按要求完成下列证明:已知:如图,AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180° .

求证:AE∥DF.
证明:∵AB∥CD()
∴∠BAC=∠DCE()
∵∠BAC+∠CDF=180°(已知),
∴ +∠CDF=180°()
∴AE∥DF().
21.如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+6,b﹣2 ).
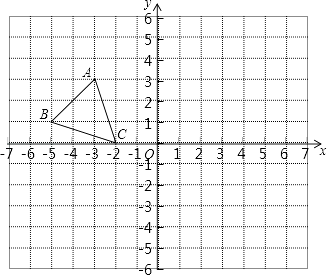 (1)、直接写出点A1 , B1 , C1的坐标.(2)、在图中画出△A1B1C1 .(3)、连接A A1 , 求△AOA1的面积.22. 关于x的方程 的解是负数,求字母k的取值范围.23. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同).若购买 个篮球和 个足球共需 元,购买 个篮球和 个足球共需 元.(1)、求篮球、足球的单价各是多少元;(2)、根据学校实际需要,需一次性购买篮球和足球共 个.要求购买篮球和足球的总费用不超过 元,则该校最多可以购买多少个篮球?24. 镇政府想了解李家庄 130 户家庭的经济情况,从中随机抽取了部分家庭进行调查,获得了他们的年收入(单位:万元),并对数据(年收入)进行整理、描述和分析.下面给出了部分信息.
(1)、直接写出点A1 , B1 , C1的坐标.(2)、在图中画出△A1B1C1 .(3)、连接A A1 , 求△AOA1的面积.22. 关于x的方程 的解是负数,求字母k的取值范围.23. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同).若购买 个篮球和 个足球共需 元,购买 个篮球和 个足球共需 元.(1)、求篮球、足球的单价各是多少元;(2)、根据学校实际需要,需一次性购买篮球和足球共 个.要求购买篮球和足球的总费用不超过 元,则该校最多可以购买多少个篮球?24. 镇政府想了解李家庄 130 户家庭的经济情况,从中随机抽取了部分家庭进行调查,获得了他们的年收入(单位:万元),并对数据(年收入)进行整理、描述和分析.下面给出了部分信息.a.被抽取的部分家庭年收入的频数分布直方图和扇形统计图如下(数据分组:0.9≤x<1.3,1.3≤x<1.7 , 1.7≤x<2.1, 2.1≤x<2.5, 2.5≤x<2.9 , 2.9≤x<3.3 )
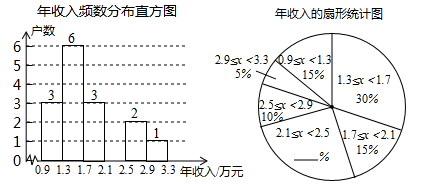
b.家庭年收入在1.3≤x<1.7 这一组的是: 1.3 1.3 1.4 1.5 1.6 1.6
根据以上信息,完成下列问题:
(1)、将两个统计图补充完整;(2)、估计李家庄有多少户家庭年收入不低于 1.5 万元且不足 2.1 万元?25. 已知:如图1,AB∥CD,点E,F分别为AB,CD上一点.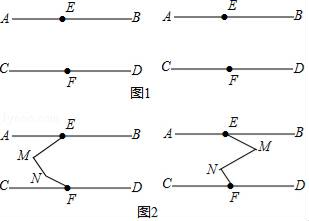 (1)、在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系.请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明;(2)、如图2,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).
(1)、在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系.请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明;(2)、如图2,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).