广东省广州市番禺区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，为无理数的是（）

A、 $\sqrt{2}$ B、3.14 C、 $| - 2 |$ D、 ${(- 2)}^{2}$

查看试题解析
2. 下列调查中，适宜全面调查的是（）

A、调查市场上某种食品的色素含量是否符合国家标准 B、了解我国七年级学生的身高情况 C、调查春节联欢晚会的收视率 D、飞机起飞前的安全检查

查看试题解析
3. 在平面直角坐标系中，点(-2，-3)到x轴的距离是（）

A、-2 B、-3 C、2 D、3

查看试题解析
4. 若a<b，则下列不等式一定成立的是（）

A、a-5>b-5 B、-2a>-2b C、2a-5>2b-5 D、-2a>-3b

查看试题解析
5. 下列说法正确的是（）

A、±5是25的算术平方根 B、±4是64的立方根 C、-2是-8的立方根 D、(-4)²的平方根是-4

查看试题解析
6. 下列实数中，在 3 与 4 之间的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{6}$ C、 $\sqrt{25}$ D、 $\sqrt{20}$ -1

查看试题解析
7. 已知 ${\begin{cases} \end{cases} \begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 是二元一次方程 $2 x + ay = 4$ 的一组解，则a的值为（）

A、2 B、 $- 2$ C、1 D、 $- 1$

查看试题解析
8. 若实数2是关于x的一元一次不等式2x-a-2<0的一个解，则a的取值范围是（）

A、a>2 B、a<2 C、a>4 D、a>3

查看试题解析
9. 如图，点 E 在 AD 的延长线上，下列条件中能判断 AB∥CD 的是（）

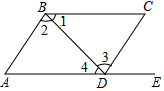A、∠1=∠4 B、∠2=∠3 C、∠C=∠CDE D、∠C+∠CDA=180°

查看试题解析
10. 如图所示，在平面直角坐标系中，A(2，0)，B(0，1)，将线段AB平移至A₁B₁的位置，则m+n的值为（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

11. 计算： $2 \sqrt{3} - \sqrt{3} =$

查看试题解析
12. 经调查，某班学生上学所用的交通工具中，自行车占60%，公交车占30%，其它占10%，用扇形图描述以上统计数据时，“公交车”对应扇形的圆心角是．

查看试题解析
13. 为了了解某校七年级600名学生的身高情况，从中抽取了50名学生进行测量，这个样本的容量(即样本中个体的数量)是．

查看试题解析
14. 如图，已知a∥b ， ∠1＝54°，则∠2的度数为．

查看试题解析
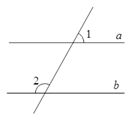15. 一条船顺流航行，每小时行驶20千米；逆流航行，每小时行驶16千米若水的流速与船在静水中的速度都是不变的，则轮船在静水中的速度为千米/小时．

查看试题解析
16. 苹果的进价是19元/千克，销售中估计有5%的苹果正常损耗，为了避免亏本，售价至少应定为元/千克．

查看试题解析

三、解答题

17. 解下列方程组：

(1)、 ${\begin{array}{l} y = 2 x - 5 \\ 3 x + 4 y = 2 \end{array}$

(2)、 ${\begin{array}{l} 2 x - 5 y = - 3 \\ - 2 x + 3 y = - 3 \end{array}$

查看试题解析
18. 解不等式组： ${\begin{array}{l} x - 2 < 4 (x + 1) \\ \frac{x - 1}{2} \leq 1 \end{array}$

查看试题解析

19. 为了解某校七年级学生的身高情况，随机抽取部分学生的身高进行调査，得到不完整的频数分布表如表，绘成不完整的频数分布直方图如图：

身高x	频数	百分比
150≤x<155	5	10%
155≤x<160	a	20%
160≤x<165	15	30%
165≤x<170	14	b
170≤x≤175	6	12%
合计		100%

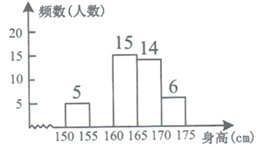
根据所给信息，解答下列问题：

(1)、求a，b的值；

(2)、补全频数分布直方图；

(3)、该校九年级共有500名学生，男生约占60%，女生约占40%，学校准备组建年级女子篮球队，要求身高不低于170cm，估计候选的女生有多少人?

查看试题解析

20. 如图，直线CD与直线AB相交于C，解答下列问题.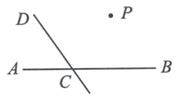

(1)、过点P画PQ∥CD，交AB于点Q；

(2)、过点P画PR⊥CD，垂足为R，连接PC，判断PC与PR的大小，并说明理由

查看试题解析
21. 如图，一只乌鸦从其巢(点O)飞出，飞向其巢东6km北10km的一点A，在该点它发现有一个稻草人，所以就转向，再向东8km北4km的地方B飞去．在那里它吃了一些谷物后立即返巢O，假设乌鸦总是沿直线飞行的，则乌鸦所飞的路径构成了一个三角形OAB

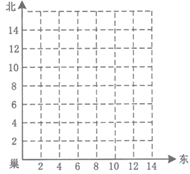(1)、若点O的坐标为(0，0)，点A的坐标为(6，10)，写出点B的坐标．

(2)、试求三角形OAB的面积．

查看试题解析
22. 如图，∠ABD和∠BDC的平分线交于E，BE交CD于点F，∠1+∠2=90°．

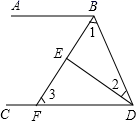(1)、求证：AB∥CD；

(2)、试探究∠2与∠3的数量关系．

查看试题解析
23. 根据市场调查，某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2：5，某厂每天生产这种消毒液22.5t．

(1)、这些消毒液应该分装大、小瓶两种产品各多少瓶?

(2)、若大、小瓶两种产品的消毒液单价分别为25元、13元，某公司需购买大、小瓶两种产品共100瓶，且购置费不多于1660元，则大瓶的消毒液最多购买多少瓶?

查看试题解析
24. 已知关于x，y的方程组 ${\begin{array}{l} 3 x - y = 2 a - 5 \\ x + 2 y = 3 a + 3 \end{array}$ 的解都为正数．

(1)、当a=2时，解此方程组；

(2)、求a的取值范围；

(3)、已知a+b=4，且b>0，z=2a-3b，求z的取值范围．

查看试题解析