山西省运城市盐湖区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,∠1与∠2是对顶角的是( )A、
2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,∠1与∠2是对顶角的是( )A、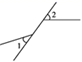 B、
B、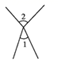 C、
C、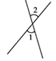 D、
D、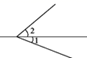 4. 冠状病毒有多种类型,新型冠状病毒也是其中的一种,有一种型冠状病毒的直径为 毫米,则数据 用科学记数法表示为( )A、 B、 C、 D、5. 已知x2+mx+25是完全平方式,则m的值为( )A、10 B、±10 C、20 D、±206. 如图,直线AB∥CD,则下列结论正确的是( )
4. 冠状病毒有多种类型,新型冠状病毒也是其中的一种,有一种型冠状病毒的直径为 毫米,则数据 用科学记数法表示为( )A、 B、 C、 D、5. 已知x2+mx+25是完全平方式,则m的值为( )A、10 B、±10 C、20 D、±206. 如图,直线AB∥CD,则下列结论正确的是( )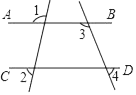 A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°7. 一只小花猫在如图的方砖上走来走去,最终停留在阴影方砖上的概率是( )
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°7. 一只小花猫在如图的方砖上走来走去,最终停留在阴影方砖上的概率是( )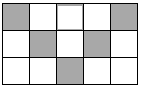 A、 B、 C、 D、8. 将一副三角尺按如图的方式摆放,其中l1∥l2 , 则∠α的度数是( )
A、 B、 C、 D、8. 将一副三角尺按如图的方式摆放,其中l1∥l2 , 则∠α的度数是( ) A、30° B、45° C、60° D、70°9. 如图,若 , .则下列各式成立的是( )
A、30° B、45° C、60° D、70°9. 如图,若 , .则下列各式成立的是( )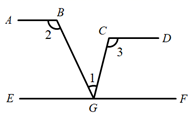 A、 B、 C、 D、10. 如图①,在矩形 中,动点P从点B出发,沿 、 、 运动至点A停止,设点P运动的路程为x, 的面积为y,如果y关于x的函数图象如图②所示,则 的面积是( )
A、 B、 C、 D、10. 如图①,在矩形 中,动点P从点B出发,沿 、 、 运动至点A停止,设点P运动的路程为x, 的面积为y,如果y关于x的函数图象如图②所示,则 的面积是( )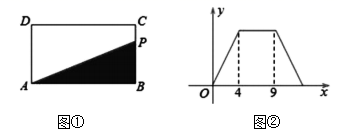 A、10 B、16 C、18 D、20
A、10 B、16 C、18 D、20二、填空题
-
11. 如图,把一根直尺与一块三角尺如图放置,若∠1=55°,则∠2的度数为.
 12. 小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程 与时间 的图像,则小明回家的速度是每分钟步行m.
12. 小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程 与时间 的图像,则小明回家的速度是每分钟步行m.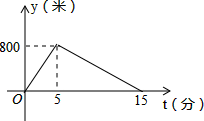 13. 一布袋中放有红、黄、绿三种颜色的球,它们除颜色外其他都一样,其中红球4个,绿球5个,任意摸出1个绿球的概率是 ,则摸出一个黄球的概率是.14. 如图,在 中, 与 的平分线相交于点O,过点O作 ,分别交 、 于点D、E,若 , ,则 的周长是 .
13. 一布袋中放有红、黄、绿三种颜色的球,它们除颜色外其他都一样,其中红球4个,绿球5个,任意摸出1个绿球的概率是 ,则摸出一个黄球的概率是.14. 如图,在 中, 与 的平分线相交于点O,过点O作 ,分别交 、 于点D、E,若 , ,则 的周长是 .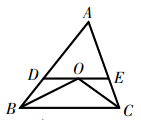 15. 如图的三角形纸片中,AB=6,AC=7,BC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长为 .
15. 如图的三角形纸片中,AB=6,AC=7,BC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED的周长为 .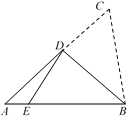
三、解答题
-
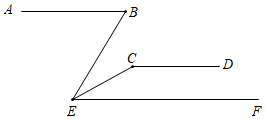
16. 计算(1)、(2)、17. 先化简,再求值:4(x﹣1)2﹣(2x+3)(2x﹣3),其中x=﹣1.18. 如图,AB∥CD∥EF , 且∠ABE=70°,∠ECD=150°,求∠BEC的度数.
 19. 某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(吨)之间关系的图象如图,根据图象回答:
19. 某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(吨)之间关系的图象如图,根据图象回答: (1)、该市自来水收费时,若使用不足5吨,则每吨收费多少元?超过5吨部分每吨收费多少元?(2)、若某户居民每月用水3.5吨,应交水费多少元?若某月交水费17元,该户居民用水多少吨?20. 某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.(1)、若小明获得1次抽奖机会,小明中奖是事件;(填随机、必然、不可能)(2)、小明观察一段时间后发现,平均每8个人中会有1人抽中一等奖,2人抽中二等奖,若袋中共有24个球,请你估算袋中白球的数量;(3)、在(2)的条件下,如果在抽奖袋中减少3个白球,那么抽奖一次恰好抽中一等奖的概率是多少?请说明理由.21. 如图,网格中的△ABC与△DEF为轴对称图形.
(1)、该市自来水收费时,若使用不足5吨,则每吨收费多少元?超过5吨部分每吨收费多少元?(2)、若某户居民每月用水3.5吨,应交水费多少元?若某月交水费17元,该户居民用水多少吨?20. 某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.(1)、若小明获得1次抽奖机会,小明中奖是事件;(填随机、必然、不可能)(2)、小明观察一段时间后发现,平均每8个人中会有1人抽中一等奖,2人抽中二等奖,若袋中共有24个球,请你估算袋中白球的数量;(3)、在(2)的条件下,如果在抽奖袋中减少3个白球,那么抽奖一次恰好抽中一等奖的概率是多少?请说明理由.21. 如图,网格中的△ABC与△DEF为轴对称图形.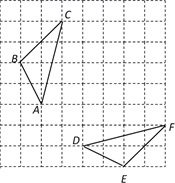 (1)、利用网格线作出△ABC与△DEF的对称轴l;(2)、结合所画图形,在直线l上画出点P,使PA+PC最小;(3)、如果每一个小正方形的边长为1,请直接写出△ABC的面积= .22. 图①是一个长为 ,宽为 的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.
(1)、利用网格线作出△ABC与△DEF的对称轴l;(2)、结合所画图形,在直线l上画出点P,使PA+PC最小;(3)、如果每一个小正方形的边长为1,请直接写出△ABC的面积= .22. 图①是一个长为 ,宽为 的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.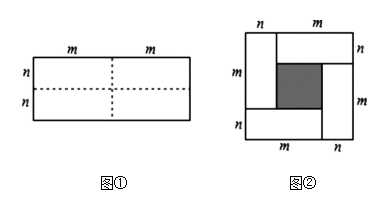 (1)、请用两种不同的方法表示图②中阴影部分的面积
(1)、请用两种不同的方法表示图②中阴影部分的面积方法一:
方法二:
(2)、观察图②,请直接写出下列三个代数式 , , 之间的等量关系;(3)、根据(2)中的等量关系,解决如下问题:若 , ,求 的值.23. 已知点C是AB上的一个动点.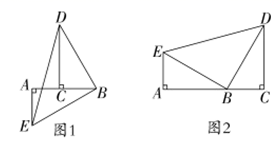 (1)、问题发现
(1)、问题发现如图1,当点C在线段AB上运动时,过点C作 ,垂足为点C,过点A作 ,垂足为点A,且 , .
① 与 全等吗?请说明理由;
②连接DE,试猜想 的形状,并说明理由;
③ 是否成立?(填“成立”或“不成立”).
(2)、类比探究如图2,当点C在线段AB的延长线上时,过点C作 ,垂足为点C,过点A作 ,垂足点A,且 , .试直接写出 的形状为;此时线段DC、AE和AC之间的数量关系为(直接写出结论,不用说明理由).