山西省吕梁市文水县2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 如图,直线AD BC,AC平分∠DAB,若∠1=65°,则∠2的度数为( )
 A、65° B、50° C、60° D、70°3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线AB,CD相交于点O,下列条件中:①∠AOD=90° ;②∠AOD=∠AOC;③∠AOC+∠BOC=180°;④∠AOC+∠BOD=180°,能说明AB⊥CD的有( )
A、65° B、50° C、60° D、70°3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线AB,CD相交于点O,下列条件中:①∠AOD=90° ;②∠AOD=∠AOC;③∠AOC+∠BOC=180°;④∠AOC+∠BOD=180°,能说明AB⊥CD的有( ) A、1个 B、2个 C、3个 D、4个5. 已知 ,则下列结论一定成立的是( )A、 B、 C、 > D、6. 为证明数轴上的点可以表示无理数,老师给同学们设计了如下方案:如图,直径为1个单位长度的圆形纸片从原点沿数轴向右滚动一周,圆上一点由原点(记为点O)到达点A,点A对应的数是多少?同学们很快想到OA的长就是这个圆的周长 ,所以点A对应的数是 ,这样无理数 就可以用数轴上的点表示出来了,上述方案中体现的数学思想是( )
A、1个 B、2个 C、3个 D、4个5. 已知 ,则下列结论一定成立的是( )A、 B、 C、 > D、6. 为证明数轴上的点可以表示无理数,老师给同学们设计了如下方案:如图,直径为1个单位长度的圆形纸片从原点沿数轴向右滚动一周,圆上一点由原点(记为点O)到达点A,点A对应的数是多少?同学们很快想到OA的长就是这个圆的周长 ,所以点A对应的数是 ,这样无理数 就可以用数轴上的点表示出来了,上述方案中体现的数学思想是( )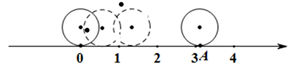 A、数形结合思想 B、分类讨论思想 C、方程思想 D、整体思想7. 不等式组 的解集在数轴上表示为( )A、
A、数形结合思想 B、分类讨论思想 C、方程思想 D、整体思想7. 不等式组 的解集在数轴上表示为( )A、 B、
B、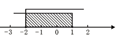 C、
C、 D、
D、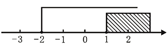 8. 若点P(m+2,2m-2)在x轴上,则点P的坐标为( )A、(0,-6) B、(3,0) C、(1,0) D、(0,-2)9. 把一根长为13m的绳子截成1m和2m两种规格的小段,要求每种规格的绳子至少有一根,且无余料,则有( )种不同的截法A、4种 B、5种 C、6种 D、7种10. 如图所示,动点P在平面直角坐标系中,按箭头所示方向呈台阶状移动,第一次从原点运动到点(0,1),第二次接着运动到点(1,1),第三次接着运动到点(1,2),……,按这样的运动规律,经过2020次运动后,动点P的坐标是( )
8. 若点P(m+2,2m-2)在x轴上,则点P的坐标为( )A、(0,-6) B、(3,0) C、(1,0) D、(0,-2)9. 把一根长为13m的绳子截成1m和2m两种规格的小段,要求每种规格的绳子至少有一根,且无余料,则有( )种不同的截法A、4种 B、5种 C、6种 D、7种10. 如图所示,动点P在平面直角坐标系中,按箭头所示方向呈台阶状移动,第一次从原点运动到点(0,1),第二次接着运动到点(1,1),第三次接着运动到点(1,2),……,按这样的运动规律,经过2020次运动后,动点P的坐标是( )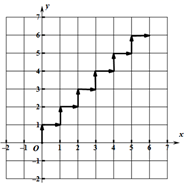 A、(2020,2020) B、(505,505) C、(1010,1010) D、(2020,2021)
A、(2020,2020) B、(505,505) C、(1010,1010) D、(2020,2021)二、填空题
-
11. 8的立方根是 .12. 山西地质博物馆是山西唯一一家普及矿产资源和地球科学知识的博物馆,为了解全省人民参观山西地质博物馆的情况,宜采用的方式调查.(填“普查”或“抽样调查”)
 13. 周末,父子二人去游泳馆游泳,当两人并排垂直站立于游泳池中时,爸爸露出水面的高度是他自身身高的 ,儿子露出水面的高度是他自身身高的 ,父子二人的身高之和为3.2米,若设父亲的身高为x米,儿子的身高为y米,则根据题意可列方程组为 .14. 若关于x,y的二元一次方程组 的解满足 ,则a的取值范围是 .15. 在平面直角坐标系中,点A的坐标为(3,0),点B为y轴右侧一点,到y轴的距离为2,且O,A,B三点构成的三角形面积为 ,则点B的坐标为 .
13. 周末,父子二人去游泳馆游泳,当两人并排垂直站立于游泳池中时,爸爸露出水面的高度是他自身身高的 ,儿子露出水面的高度是他自身身高的 ,父子二人的身高之和为3.2米,若设父亲的身高为x米,儿子的身高为y米,则根据题意可列方程组为 .14. 若关于x,y的二元一次方程组 的解满足 ,则a的取值范围是 .15. 在平面直角坐标系中,点A的坐标为(3,0),点B为y轴右侧一点,到y轴的距离为2,且O,A,B三点构成的三角形面积为 ,则点B的坐标为 .三、解答题
-
16. 计算.(1)、解方程组(2)、解不等式17. 已知:实数a为 的小数部分,b是9的平方根,求式子 的值.18. 如图,在平面直角坐标系中,已知点A(0,-2),B(3,-1),将线段AB先向左平移2个单位长度,再向上平移3个单位长度得到线段A1B1 .
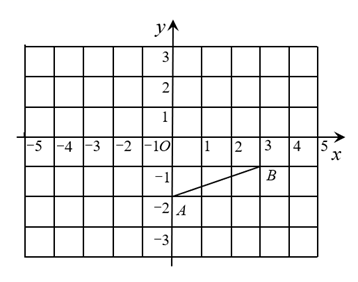 (1)、请直接写出A,B两点的对应点A1 , B1的坐标;(2)、在平面直角坐标系中画出线段A1B1;(3)、连接OA1 , OB1 , 求三角形A1OB1的面积.19. 学校为了解疫情期间学生自习课落实“停课不停学,学习不延期”在线学习的效果,王校长通过网络学习平台,随机抽查了该校部分学生在一节自习课中的学习情况,发现共有四种学习方式(每人只参与其中一种):A:阅读电子读物,B:听教师录播课程,C:完成在线作业,D:线上讨论交流.并根据调查结果绘制成如下两幅不完整的统计图,根据图中信息,解答下列问题:
(1)、请直接写出A,B两点的对应点A1 , B1的坐标;(2)、在平面直角坐标系中画出线段A1B1;(3)、连接OA1 , OB1 , 求三角形A1OB1的面积.19. 学校为了解疫情期间学生自习课落实“停课不停学,学习不延期”在线学习的效果,王校长通过网络学习平台,随机抽查了该校部分学生在一节自习课中的学习情况,发现共有四种学习方式(每人只参与其中一种):A:阅读电子读物,B:听教师录播课程,C:完成在线作业,D:线上讨论交流.并根据调查结果绘制成如下两幅不完整的统计图,根据图中信息,解答下列问题: (1)、王校长本次抽查了名学生;(2)、将条形统计图补充完整;(3)、求扇形统计图中“C:完成在线作业”对应的圆心角的度数;(4)、该校在线学习的学生共有3200名,请估计当时全校“B:听教师录播课程”的约有多少名学生?20. 完成下列推理过程.
(1)、王校长本次抽查了名学生;(2)、将条形统计图补充完整;(3)、求扇形统计图中“C:完成在线作业”对应的圆心角的度数;(4)、该校在线学习的学生共有3200名,请估计当时全校“B:听教师录播课程”的约有多少名学生?20. 完成下列推理过程.已知:如图,∠1+∠2=180°, ∠3=∠B.
求证: ∠EDG+∠DGC=180°
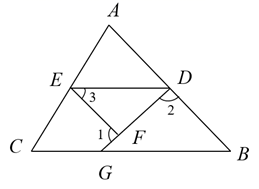
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2=∠DFE( )
∴EF AB( )
∴∠3= ( )( )
又∵∠3=∠B(已知)
∴∠B= ( )( )
∴DE BC( )
∴∠EDG+∠DGC=180°( )
21. 对于实数a,b规定了一种新的运算“※”:※ = ,
例如:4※3= =5,2※3=2×3=6
若x,y满足方程组 ,求y※(x※y)的值.
22. 为更好地推进生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役全面打响.为此某小区准备购买A、B两种型号的垃圾箱,通过对市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需390元,购买2个A型垃圾箱比购买1个B型垃圾箱少用20元. (1)、求每个A型垃圾箱和每个B型垃圾箱分别多少元?(2)、该小区物业计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个,则该小区最多可以购买B型垃圾箱多少个?23. 综合与探究
(1)、求每个A型垃圾箱和每个B型垃圾箱分别多少元?(2)、该小区物业计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个,则该小区最多可以购买B型垃圾箱多少个?23. 综合与探究问题情境
在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
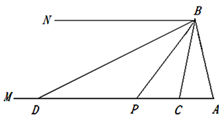 (1)、探索发现
(1)、探索发现“快乐小组”经过探索后发现:
当∠A=60º时,∠CBD=∠A.请说明理由.
(2)、不断改变∠A的度数,∠CBD与∠A却始终存在某种数量关系,用含∠A的式子表示∠CBD为 .(3)、操作探究“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变,请写出它们的关系,并说明理由.
(4)、点P继续在射线AM上运动,当运动到使∠ACB=∠ABD时,请直接写出2∠ABC+ ∠A的结果.