广东省深圳市龙岗区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-16 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $x^{_{2}} \cdot x^{_{3}}$ 符合题意结果是（　　）

A、 $x^{_{4}}$ B、 $x^{_{5}}$ C、 $x^{_{6}}$ D、 $x^{7}$

查看试题解析
2. 下列交通标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列事件中，是必然事件的是（）

A、从装有10个黑球的不透明袋子中摸出一个球，恰好是红球 B、抛掷一枚普通正方体骰子，所得点数小于7 C、抛掷一枚一元硬币，正面朝上 D、从一副没有大小王的扑克牌中抽出一张，恰好是方块

查看试题解析
4. 成人体内成熟的细胞的平均直径一般为0.00000073m ，可以用科学记数法表示为（　　）

A、 $7.3 \times 10^{_{6}} m$ B、 $7.3 \times 10^{_{7}} m$ C、 $7.3 \times 10^{_{- 6}} m$ D、 $7.3 \times 10^{_{- 7}} m$

查看试题解析
5. 以下列各组线段为边，能组成三角形的是（）

A、2cm，3cm，5cm B、5cm，6cm，10cm C、1cm，1cm，3cm D、3cm，4cm，9cm

查看试题解析
6. 下列运算正确的是（　　）

A、 ${(a b)}^{_{2}} = a^{_{2}} b^{_{2}}$ B、 ${(a^{_{2}})}^{3} = a^{_{5}}$ C、 $a^{_{6}} \div a^{_{2}} = a^{_{3}}$ D、 $a^{- 2} = - \frac{1}{a^{_{2}}}$

查看试题解析
7. 如果等腰三角形的一个内角为50°，那么其它两个内角为（）

A、50°，80° B、65°，65° C、50°，65° D、50°，80°或 65°，65°

查看试题解析
8. 如图，下列条件中能判定直线l₁∥l₂的是（）

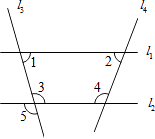A、∠1=∠2 B、∠1=∠5 C、∠1+∠3=180° D、∠3=∠5

查看试题解析
9. 下列各式中，不能运用平方差公式进行计算的是（）

A、 $(2 x - 1) (- 1 + 2 x)$ B、 $(a b - 1) (a b + 1)$ C、 $(- 2 x - y) (2 x - y)$ D、 $(- a + 5) (- a - 5)$

查看试题解析
10. 已知 $x + y = 3$ ， $x y = - 2$ ，则 $x^{_{2}} - x y + y^{_{2}}$ 的值是（　　）

A、11 B、15 C、3 D、7

查看试题解析
11. 甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系图象如图所示，根据图中提供的信息，有下列说法：

⑴他们都行驶了18千米；

⑵甲在途中停留了0.5小时；

⑶乙比甲晚出发了0.5小时；

⑷相遇后，甲的速度小于乙的速度；

⑸甲、乙两人同时到达目的地

其中符合图象描述的说法有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
12. 如图，在 $R t Δ A C B$ 中， $∠ A C B = 90 °$ ， $Δ A B C$ 的角平分线 $A D$ ， $B E$ 相交于点P，过点P作 $P F ⊥ A D$ 交 $B C$ 的延长线于点F，交 $A C$ 于点H．则下列结论：① $∠ A P B = 135 °$ ；② $B F = B A$ ；③ $P 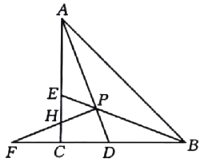H = P D$ ；④连接 $C P$ ， $C P$ 平分 $∠ A C B$ ．其中正确的是（）．

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

13. 计算：x（x﹣2）＝

查看试题解析
14. 如图，已知∠ACB=∠DBC ，要用“SAS”判断△ABC≌△DCB ，需添加的一个条件：．

查看试题解析
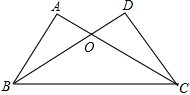15. 如图所示，已知△ABC的周长是30，OB ， OC分别平分∠ABC和∠ACB ， OD⊥BC于D ，且OD=3，则△ABC的面积是．

查看试题解析
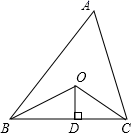16. 如图，A、B、C分别是线段A₁B ， B₁C ， C₁A的中点，若 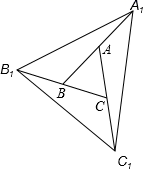$△ A B C$ 的面积是3，那么 $△ A_{1} B_{1} C_{1}$ 的面积是．

查看试题解析

三、解答题

17. 计算：

(1)、 $(6 a^{_{3}} b^{_{2}} - 4 a^{_{2}} b) \div 2 a b$

(2)、 $- 1^{_{^{2018}}} + {(\frac{1}{2})}^{_{- 2}} + {(3.14 - π)}^{_{0}}$

查看试题解析
18. 先化简，再求值： ${(2 a - 1)}^{2} + (a + 1) (a - 1) - 4 a (a - 1),$ 其中 $a = - 1$ .

查看试题解析
19. 在一个不透明的袋中装有3个红球，4个黄球和若干白球，它们除颜色外其他都相同，将球搅匀，从中任意摸出一个球．

(1)、若袋内有5个白球，从中任意摸出一个球，是红球的概率为，是黄球的概率为，是白球的概率为．

(2)、如果任意摸出一个球是黄球的概率是 $\frac{2}{5}$ ，求袋中内有几个白球？

查看试题解析
20. 为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成下表：

汽车行驶时间t（h）

0

1

2

3

…

油箱剩余油量Q（L）

100

94

88

82

…

(1)、在这个变化过程中，是自变量，是因变量；（填中文）

(2)、根据上表的数据，请你写出Q与t的关系式：；

(3)、汽车行驶6h后，油箱中的剩余油量是；

(4)、该品牌汽车的油箱加满60L ，若以100km/h的速度匀速行驶，该车最多能行驶km ．

查看试题解析
21. 如图，在△ABC中，AB=AC ， AB的垂直平分线MN交AC于点D ，交AB于点E ．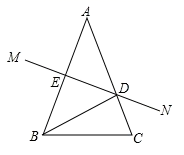

(1)、若∠A=40°，求∠DBC的度数；

(2)、若AE=4，△CBD的周长为20，求BC的长．

查看试题解析
22. 如图，点O为线段AB上的任意一点（不于A、B重合），分别以AO ， BO为一腰在AB的同侧作等腰△AOC和△BOD ， OA=OC ， OB=OD ， ∠AOC与∠BOD都是锐角，且∠AOC=∠BOD ， AD与BC交于点P ， AD交CO于点M ， BC交DO于点N ．

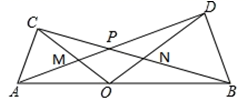(1)、试说明：CB=AD；

(2)、若∠COD=70°，求∠APB的度数．

查看试题解析
23. 直角三角形ABC中，∠ACB=90°，直线l过点C ．

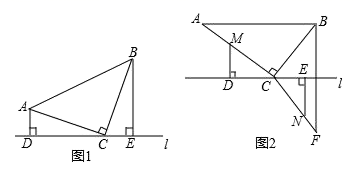(1)、当AC=BC时，如图①，分别过点A、B作AD⊥l于点D ， BE⊥l于点E ．求证：△ACD≌△CBE ．

(2)、当AC=8，BC=6时，如图②，点B与点F关于直线l对称，连接BF ， CF ，动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动，同时动点N从点F出发，以每秒3个单位的速度沿F→C→B→C→F向终点F运动，点M、N到达相应的终点时停止运动，过点M作MD⊥l于点D ，过点N作NE⊥l于点E ，设运动时间为t秒．
①CM= ，当N在F→C路径上时，CN= ．（用含t的代数式表示）

②直接写出当△MDC与△CEN全等时t的值．

查看试题解析

汽车行驶时间t（h）	0	1	2	3	…
油箱剩余油量Q（L）	100	94	88	82	…