广东省广州市越秀区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-16 类型:期末考试
一、单选题
-
1. 在平面直角坐标系 中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列调查中,适宜采用全面调查的是( ).A、调查某池墙中现有鱼的数量 B、调查某批次汽车的抗撞击能力 C、选出某班短跑最快的学生参加全校短跑比赛 D、调查市场上某种食品的色素含量是否符合国家标准3. 下列判断正确的是( )A、 B、 C、 D、4. 如图,ABCD是四边形,下列条件中可以判定 的是( )
 A、 B、 C、 D、5. 由 可以得到用 表示 的式子为( )A、 B、 C、 D、6. 下列命题中是假命题的是( )A、若 ,则 B、若 ,则x是一个无理数 C、若 ,则 D、若 ,则7. 如果点 在第二象限,那么m的取值范围是( )A、 B、 C、 D、8. 如图,将 向右平移 ,得到 ,若 的周长为 ,则四边形ABFD的周长是( )
A、 B、 C、 D、5. 由 可以得到用 表示 的式子为( )A、 B、 C、 D、6. 下列命题中是假命题的是( )A、若 ,则 B、若 ,则x是一个无理数 C、若 ,则 D、若 ,则7. 如果点 在第二象限,那么m的取值范围是( )A、 B、 C、 D、8. 如图,将 向右平移 ,得到 ,若 的周长为 ,则四边形ABFD的周长是( )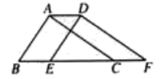 A、 B、 C、 D、9. 如图,已知 , , ,则 的度数为( )
A、 B、 C、 D、9. 如图,已知 , , ,则 的度数为( ) A、 B、 C、 D、10. 如果关于x的不等式组 的整数解仅为3,4,5,那么适合这个不等式组的整数对 共有( )A、8对 B、12对 C、15对 D、20对
A、 B、 C、 D、10. 如果关于x的不等式组 的整数解仅为3,4,5,那么适合这个不等式组的整数对 共有( )A、8对 B、12对 C、15对 D、20对二、填空题
-
11. 某校学生来自甲、乙、丙三个地区,其人数比为5:4:3,如图所示的扇形图表示上述分布情况,则“来自甲地区的学生”对应扇形的圆心角的度数为 .
 12. 已知 , 是方程 的解,则a的值是 .13. 如图, , , ,则 的度数为 .
12. 已知 , 是方程 的解,则a的值是 .13. 如图, , , ,则 的度数为 . 14. 如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(-3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 .
14. 如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(-3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 .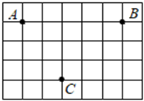 15. 若 ,则 的立方根是 .16. 甲和乙同时从A地出发,匀速行走到B地.甲走完一半路程时,乙才走了4千米.乙走完一半路程时,甲已走了9千米.当甲走完全程时,乙未走完的路程还有千米
15. 若 ,则 的立方根是 .16. 甲和乙同时从A地出发,匀速行走到B地.甲走完一半路程时,乙才走了4千米.乙走完一半路程时,甲已走了9千米.当甲走完全程时,乙未走完的路程还有千米三、解答题
-
17. 如图,已知 ,点P在 的内部,用三角板与量角器作图,并回答问题:
 (1)、过点P作 ,交 于C,并求 的度数;(2)、过点P作 ,垂足为D,连接 ,并比较线段 与 的大小.18. 求下列各式中x的值;(1)、25x2=4(2)、19. 解不等式组 并把解集在数轴上表示出来.20. 某家庭记录了使用节水龙头的日用水量样本数据(单位: ),得到频数分布表如下:
(1)、过点P作 ,交 于C,并求 的度数;(2)、过点P作 ,垂足为D,连接 ,并比较线段 与 的大小.18. 求下列各式中x的值;(1)、25x2=4(2)、19. 解不等式组 并把解集在数轴上表示出来.20. 某家庭记录了使用节水龙头的日用水量样本数据(单位: ),得到频数分布表如下:日用水量
频数
百分比
1
2
6
3
 (1)、求 的值;(2)、补全频数分布直方图;(3)、估计该家庭使用节水龙头100天后,其中日用水量小于 的天数是多少天?21. 如图,在平面直角坐标系 中, 的三个顶点的坐标分别是 , , ,将 先向下平移5个单位长度,然后向右平移6个单位长度,再作关于x轴对称的图形,得到 .
(1)、求 的值;(2)、补全频数分布直方图;(3)、估计该家庭使用节水龙头100天后,其中日用水量小于 的天数是多少天?21. 如图,在平面直角坐标系 中, 的三个顶点的坐标分别是 , , ,将 先向下平移5个单位长度,然后向右平移6个单位长度,再作关于x轴对称的图形,得到 . (1)、写出点 的坐标;(2)、在平面直角坐标系 中画出 ;(3)、求 的面积.
(1)、写出点 的坐标;(2)、在平面直角坐标系 中画出 ;(3)、求 的面积.
