陕西省西安市莲湖区2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2020-09-16 类型：期中考试

进入出卷网下载

一、选择题

1. 25的算术平方根是（　　）

A、5 B、﹣5 C、±5 D、 $\sqrt{5}$

查看试题解析
2. 在3.14159， $\frac{22}{7}$ ，0，π，0.101001……（每两个1之间依次增加1个0）这5个数中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在平面直角坐标系中，点P（3，﹣2）到y轴的距离为（）

A、3 B、﹣3 C、2 D、﹣2

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{8}$ ＝3 $\sqrt{2}$ B、 $\sqrt{2}$ + $\sqrt{3}$ ＝ $\sqrt{5}$ C、4 $\sqrt{3}$ ﹣3 $\sqrt{3}$ ＝1 D、3+2 $\sqrt{2}$ ＝5 $\sqrt{2}$

查看试题解析
5. 比较两个实数 $\frac{\sqrt{5} - 1}{2}$ 与 $\frac{1}{2}$ 的大小，下列正确的是（）

A、 $\frac{\sqrt{5} - 1}{2} > \frac{1}{2}$ B、 $\frac{\sqrt{5} - 1}{2} < \frac{1}{2}$ C、 $\frac{\sqrt{5} - 1}{2} = \frac{1}{2}$ D、 $\frac{\sqrt{5} - 1}{2} 与 \frac{1}{2}$ 的大小不确定

查看试题解析
6. 在平面直角坐标系中，点P（2m+3，3m﹣1）在正比例函数y＝x的图象上，则m的值为（）

A、 $- \frac{2}{5}$ B、 $\frac{1}{3}$ C、 $\frac{3}{2}$ D、4

查看试题解析
7. 已知关于x的一次函数y＝（2﹣m）x+2的图象如图所示，则实数m的取值范围为（）

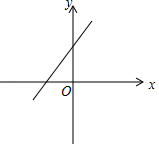A、m＞2 B、m＜2 C、m＞0 D、m＜0

查看试题解析
8. 如图，在四边形ABCD中，AB＝BC＝2 $\sqrt{2}$ ，AD＝2，∠B＝∠D＝90°，则CD等于（）

A、2 B、 $\sqrt{6}$ C、2 $\sqrt{3}$ D、 $\sqrt{14}$

查看试题解析
9. 如图所示的是一辆汽车行驶的速度（千米/时）与时间（分）之间的变化图，下列说法正确的是（）

A、时间是因变量，速度是自变量 B、汽车在1～3分钟时，匀速运动 C、汽车最快的速度是30千米/时 D、汽车在3～8分钟静止不动

查看试题解析
10. 如图，在平面直角坐标系中有一个3×3的正方形网格，其右下角格点（小正方形的顶点）A的坐标为（﹣1，1），左上角格点B的坐标为（﹣4，4），若分布在过定点（﹣1，0）的直线y＝﹣k（x+1）两侧的格点数相同，则k的取值可以是（）

A、 $\frac{5}{2}$ B、 $\frac{7}{4}$ C、2 D、 $\frac{3}{2}$

查看试题解析

二、填空题

11. 已知函数y＝2x^m^﹣¹+1是一次函数，则m＝.

查看试题解析
12. 已知A（a﹣5，2b﹣1）在y轴上，B（3a+2，b+3）在x轴上，则C（a，b）的坐标为.

查看试题解析
13. 已知 $\sqrt{a - 17}$ +2 $\sqrt{17 - a}$ ＝b+8，则 $\sqrt{a - b}$ 的值是.

查看试题解析
14. 如图，在平面直角坐标系中，一巡查机器人接到指令，从原点O出发，沿O→A₁→A₂→A₃→A₄→A₅→A₆→A₇→A₈…的路线移动，每次移动1个单位长度，依次得到点A₁（0，1），A₂（1，1），A₃（1，0），A₄（2，0），A₅（2，﹣1），A₆（3，﹣1），A₇（3，0），A₈（4，0），…若机器人巡查到某一位置的横坐标为23时，即停止，则其纵坐标为.

查看试题解析

三、解答题

15. 计算： $\sqrt{18} - 2 \sqrt{\frac{1}{8}} + \frac{1}{4} \sqrt{32}$

查看试题解析
16. 计算：（2 $\sqrt{5}$ +5 $\sqrt{2}$ ）（2 $\sqrt{5}$ ﹣5 $\sqrt{2}$ ）﹣（ $\sqrt{5}$ ﹣ $\sqrt{2}$ ）²﹣2 $\sqrt{10}$ .

查看试题解析
17. 求式子2（x﹣1）²﹣18＝0中x的值.

查看试题解析
18. 如图，直线l垂直数轴于原点在数轴上，用尺规作出表示 $- \sqrt{13}$ 的点E（不写作法，保留作图痕迹）.

查看试题解析
19. 已知a+3和2a﹣15是某正数的两个平方根，b的立方根是﹣2，c算术平方根是其本身，求2a+b﹣3c的值．

查看试题解析
20. 如图，在平面直角坐标系中△ABC各顶点的坐标分别为A（4，0），B（﹣1，4），C（﹣3，1）.

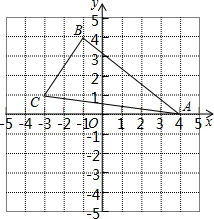(1)、在图中作△A'B'C'，使△A'B'C'与△ABC关于y轴对称；

(2)、请分别写出点A'，B'，C'的坐标.

查看试题解析
21. 已知a，b，c满足（a﹣ $\sqrt{8}$ ）²+ $\sqrt{b - 4}$ + $| c - 2 \sqrt{6} |$ ＝0.

(1)、求a，b，c的值；

(2)、试判断以a，b，c为边长能否构成直角三角形，并说明理由.

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，沿AF折叠三角形使得点C落在AB边上的点D处，求CF的长.

查看试题解析
23. 如图，正比例函数y＝kx的图象经过点A，点A在第二象限.过点A作AH⊥x轴，垂足为H.已知点A的横坐标为﹣3，且△AOH的面积为4.5.

(1)、求该正比例函数的解析式.

(2)、将正比例函数y＝kx向下平移，使其恰好经过点H，求平移后的函数解析式.

查看试题解析
24. 阅读材料：像（ $\sqrt{5}$ + $\sqrt{2}$ ）（ $\sqrt{5} -$ $\sqrt{2}$ ）＝3， $\sqrt{a}$ • $\sqrt{a}$ ＝a（a≥0），（ $\sqrt{b}$ +1）（ $\sqrt{b}$ ﹣1）＝b﹣1（b≥0），……，这种两个含二次根式的代数式相乘，积不含二次根式，我们称这两个代数式互为有理化因式例如： $\sqrt{3}$ 与 $\sqrt{3}$ ， $\sqrt{2}$ +1与 $\sqrt{2}$ ﹣1，2 $\sqrt{3}$ +3 $\sqrt{5}$ 与2 $\sqrt{3}$ ﹣3 $\sqrt{5}$ 等都是互为有理化因式，在进行二次根式计算时，利用有理化因式，可以化去分母中的根号.
例如： $\frac{1}{2 \sqrt{3}} = \frac{\sqrt{3}}{2 \sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{6}$ ； $\frac{\sqrt{2} + 1}{\sqrt{2} - 1} = \frac{{(\sqrt{2} + 1)}^{2}}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = 3 + 2 \sqrt{2}$ ；

解答下列问题：

(1)、3﹣ $\sqrt{7}$ 与互为有理化因式，将 $\frac{2}{3 \sqrt{2}}$ 分母有理化得.

(2)、计算：2﹣ $\frac{1}{\sqrt{3}} - \frac{6}{\sqrt{3}}$ ；

(3)、观察下面的变形规律并解决问题.
① $\frac{1}{\sqrt{2} + 1}$ ＝ $\sqrt{2}$ ﹣1， $\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝ $\sqrt{3} -$ $\sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}}$ ＝ $\sqrt{4} - \sqrt{3}$ ，…，若n为正整数，请你猜想： $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ＝.

②计算：（ $\frac{1}{\sqrt{2} + 1}$ + $\frac{1}{\sqrt{3} + \sqrt{2}}$ + $\frac{1}{\sqrt{4} + \sqrt{3}}$ +…+ $\frac{1}{\sqrt{2020} + \sqrt{2019}}$ ）×（ $\sqrt{2020}$ +1）.

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝8cm，点P从点A出发，沿AB方向以每秒 $\sqrt{2}$ cm的速度向点B运动，同时动点Q从B点出发，以每秒1cm的速度向C点运动，设P，Q两点的运动时间为t（0＜t＜8）秒.

(1)、BQ＝， BP＝（用含t的式子表示）.

(2)、当t＝2时，求△PCQ的面积（提示：在一个三角形中，若两个角相等，则角所对的边也相等）.

(3)、当PQ＝PC时，求t的值.

查看试题解析