云南省文山州富宁县2020年数学中考模拟试卷（5月）

试卷更新日期：2020-09-16 类型：中考模拟

进入出卷网下载

一、填空题

1. －2的相反数是.

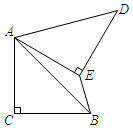
查看试题解析
2. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
3. 已知点A(1，1)在反比例函数 $y = \frac{k - 1}{2 x}$ 的图象上，则k的值为.

查看试题解析
4. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，将△ABC绕点A逆时针旋转60°，得到△ADE，连接BE，则∠BED的度数为.

查看试题解析
5. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两.问马、牛各价几何？”设马每匹 $x$ 两，牛每头 $y$ 两，根据题意可列方程组为.

查看试题解析
6. 已知等腰直角三角形ABC的BC边上的高为3，则△ABC的面积为.

查看试题解析

二、单选题

7. 第二届中国际进口博览会于2019年11月10日闭幕，本届进博会意向成交约4979亿元人民币，比首届增长23%，将数据4979亿用科学记数法表示为（）

A、 $4979 \times 10^{8}$ B、 $4.979 \times 10^{8}$ C、 $4.979 \times 10^{11}$ D、 $0.4979 \times 10^{12}$

查看试题解析
8. 下面四个图案可以看作轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
9. 六边形的内角和为（）

A、360° B、540° C、720° D、900°

查看试题解析
10. 如图，一块三角板的两个顶点放在直尺的对边上，如果∠1＝28°，那么∠2的度数是（）

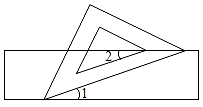A、28° B、56° C、62° D、52°

查看试题解析
11. 小欣同学对数据28，2■，48，50，52进行统计分析，发现其中一个两位数的个位数字被墨水污染看不到了，则分析结果与被污染数字无关的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
12. 观察列数：﹣2，8，﹣32，128……按照这列数的排列规律，第n个数应该是（）

A、（﹣2）ⁿ B、（﹣2）²ⁿ^﹣¹ C、﹣2²ⁿ^﹣¹ D、（﹣1）ⁿ•2²ⁿ^﹣¹

查看试题解析
13. 如图，∠ACB是⊙O的圆周角，若⊙O的半径为10，∠ACB＝45°，则扇形AOB的面积为（）

A、5π B、12.5π C、20π D、25π

查看试题解析
14. 抛物线y＝ax²＋bx＋c（a，b，c为常数，a＜0）经过点(0，2)，且关于直线x＝﹣1对称，（x₁ ， 0）是抛物线与x轴的一个交点，有下列结论，其中结论错误的是（）

A、方程ax²＋bx＋c＝2的一个根是x＝﹣2 B、若x₁＝2，则抛物线与x轴的另一个交点为(﹣4，0) C、若m＝4时，方程ax²＋bx＋c＝m有两个相等的实数根，则a＝﹣2 D、若 $- \frac{3}{2}$ ≤x≤0时，2≤y≤3，则a＝ $- \frac{1}{2}$

查看试题解析

三、解答题

15. 计算： $\sqrt{8} - 4 \sin 45^{°} + {(- 1)}^{2} - 2^{- 1}$

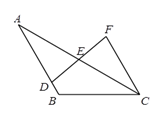
查看试题解析
16. 如图，点D是AB上一点，DF交AC于点E， DE＝FE，FC∥AB.求证：AE＝CE.

查看试题解析
17. 某校在向贫困地区捐书活动中全体师生积极捐书.为了解所捐书籍的种类，某同学对部分书籍进行了抽样调查，并根据调查数据绘制了如图所示不完整统计图.请根据统计图回答下面问题：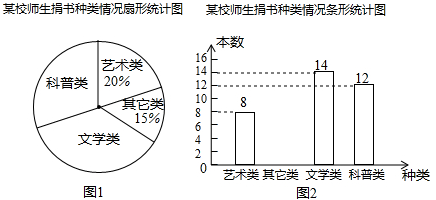

(1)、本次抽样调查的书籍有多少本？请通过计算补全条形统计图；

(2)、求出图 $1$ 中表示科普类书籍的扇形圆心角度数；

(3)、本次活动师生共捐书 $2000$ 本，请估计有多少本文学类书籍？

查看试题解析
18. 为了全面推进青少年素质教育，我市某中学组织八年级学生前往距学校 $10 km$ 的“示范性综合实践基地”开展社会实践活动.一部分学生骑自行车先走，过了 $20 min$ 后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.

查看试题解析
19. 某公司选派两人参加年度培训，小颖妈妈、张阿姨、李阿姨和王阿姨都报了名，若从4人中随机选派2人

(1)、“小颖被选派”是事件，“小颖妈妈被选派”是事件.（填“不可能”或“必然“或“随机”）

(2)、试用画树状图或列表的方法表示这次选派所有可能的结果，并求出“小颖妈妈被选派”的概率.

查看试题解析
20. 如图，在▱ABCD中，BC＝10，对角线AC⊥AB，点EF在BC、AD上，且BE＝DF.

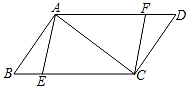(1)、求证：四边形AECF是平行四边形；

(2)、当四边形AECF是菱形时，求BE的长.

查看试题解析
21. 我们给抛物线y＝a（x﹣h）²＋k（a≠0）定义一种变换，先作这条抛物线关于原点对称的抛物线 $y^{'}$ ，再将得到的对称抛物线 $y^{'}$ 向上平移m（m＞0）个单位长度，得到新的抛物线y_m ，则我们称y_m为二次函数y＝a（x﹣h）²＋k（a≠0）的m阶变换.若抛物线M的6阶变换的关系式为 $y_{6} = {(x - 1)}^{2} + 5$ .

(1)、抛物线M的函数表达式为；

(2)、若抛物线M的顶点为点A，与r轴相交的两个交点中的左侧交点为点B，则在抛物线 $y_{6} = {(x - 1)}^{2} + 5$ 上是否存在点P，使点P与直线AB的距离最短？若存在，请求出此时点P的坐标.

查看试题解析
22. 如图所示的是一个宽5米的餐厅，只能放8张餐桌.现计划扩建增加座位，只能对原宽度进行加长，设加长后的长度为m米.若餐厅的餐桌数为y，经计算，得到如下数据：（注：m和y都为正整数）

m（米）

5

8

11

14

……

餐桌数y（张）

8

12

16

……

(1)、根据表中数据的规律，完成以上表格；

(2)、求出y关于m的函数解析式；

(3)、若这家餐厅至少要有80张餐桌，求m的最小值.

查看试题解析
23. 如图，AB为⊙O的直径，AC，BC是⊙O的两条弦，过点C作∠BCD＝∠A，CD交AB的延长线于点D.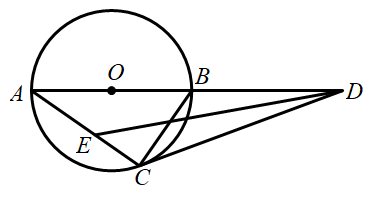

(1)、试说明：CD是⊙O的切线；

(2)、若tanA＝ $\frac{3}{4}$ ，求 $\frac{B D}{A B}$ 的值；

(3)、在（2）的条件下，若AB＝7，DE平分∠ADC交AC于点E，求ED的长.

查看试题解析

m（米）	5	8	11	14	……
餐桌数y（张）	8	12	16		……