云南省昆明市2020年数学中考适应性试卷(四)
试卷更新日期:2020-09-16 类型:中考模拟
一、填空题
-
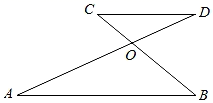
1. -2019的相反数是.2. 如图,已知AD与BC相交于点O,AB∥CD.若∠B=40°,∠D=25°,则∠COD的大小为.
 3. 预计于2020年通车的昆明地铁2号线二期工程,北起于环城南路站,终止于宝丰村站,全长12748米,数据12748用科学记数法表示为.4. 按规律排列的一列数: , , , , ,…,则第2020个数是.5. 如图,从一块圆形铁皮上剪出一个圆心角为90°的扇形,已知该扇形的面积为2π,则该扇形铁皮的半径为.
3. 预计于2020年通车的昆明地铁2号线二期工程,北起于环城南路站,终止于宝丰村站,全长12748米,数据12748用科学记数法表示为.4. 按规律排列的一列数: , , , , ,…,则第2020个数是.5. 如图,从一块圆形铁皮上剪出一个圆心角为90°的扇形,已知该扇形的面积为2π,则该扇形铁皮的半径为. 6. 如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+ (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为.
6. 如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+ (a>0)与y轴交于点A,过点A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为.
二、单选题
-
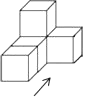
7. 下列计算正确的是( )A、x2•x3=x6 B、(x2)3=x5 C、x2+x3=x5 D、x6÷x3=x38. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间9. 由五个相同的立方体搭成的几何体如图所示,则它的左视图是( )
 A、
A、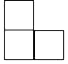 B、
B、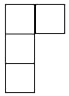 C、
C、 D、
D、 10. 多项式3x2y﹣6y在实数范围内分解因式正确的是( )A、 B、3y(x2﹣2) C、y(3x2﹣6) D、11. 求方程x2﹣x﹣6=0的根的个数( )A、没有实根 B、两个不相等的实数根 C、两个相等的实数根 D、无法确定12. 如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=( )
10. 多项式3x2y﹣6y在实数范围内分解因式正确的是( )A、 B、3y(x2﹣2) C、y(3x2﹣6) D、11. 求方程x2﹣x﹣6=0的根的个数( )A、没有实根 B、两个不相等的实数根 C、两个相等的实数根 D、无法确定12. 如图,四边形ABCD为平行四边形,E、F为CD边的两个三等分点,连接AF、BE交于点G,则S△EFG:S△ABG=( )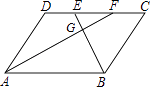 A、1:3 B、3:1 C、1:9 D、9:113. 如图, 的顶点 在反比例函数 的图像上,顶点 在 轴上, 轴,若点 的坐标为 , ,则 的值为( )
A、1:3 B、3:1 C、1:9 D、9:113. 如图, 的顶点 在反比例函数 的图像上,顶点 在 轴上, 轴,若点 的坐标为 , ,则 的值为( ) A、4 B、-4 C、7 D、-714. 如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
A、4 B、-4 C、7 D、-714. 如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是: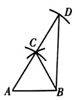
①作线段AB,分别以 为圆心,以AB长为半径作弧,两弧的交点为C;
②以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
③连接
下列说法不正确的是( )
A、 B、 C、点 是 的外心 D、三、解答题
-
15. 计算: .16. 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.求证:AB=AC.
 17. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
17. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息..A课程成绩的频数分布直方图如下(数据分成6组: , , , , , );

.A课程成绩在 这一组是:
70 71 71 71 76 76 77 78 79 79 79
.A,B两门课程成绩的平均数、中位数、众数如下:
课程
平均数
中位数
众数
A
B
70
83
根据以上信息,回答下列问题:
(1)、写出表中 的值;(2)、在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是(填“A”或“B”),理由是;(3)、假设该年级学生都参加此次测试,估计A课程成绩超过 分的人数.
18. 现有三张正面分别标有数字3,4,5的卡片(注:三张卡片的形状、大小、质地等方面完全相同,若背面朝上放在桌面上,这三张卡片看上去毫无差别)洗匀后,背面向上放在桌面上,先由甲从中随机抽取一张卡片,记录该卡片上的数字后放回洗匀,再由乙随机抽取一张卡片.若两人抽取的数字和为2的倍数,则甲获胜;否则乙获胜.(1)、用列表法或画树状图法(树状图也称树形图)中的一种方法表示出所有等可能的结果;(2)、问甲和乙谁获胜的可能性更大?请说明理由.19. 某种汽车油箱的容量为250升,开始出发后在平路上匀速行驶了4小时,汽车油箱的剩余油量是150升;之后该车又在上坡路上匀速行驶了2小时,此时汽车油箱的剩余油量是90升.这种汽车油箱的剩余油量y(升)与行驶时间x(小时)之间的部分函数图象如图所示. (1)、求y与x的函数解析式(也称关系式),并直接写出自变量x的取值范围;(2)、如果6.5小时后该车还一直在上坡路上匀速行驶,问最多还能够行驶多少小时?20. 如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时该同学距地面的高度AE为27米,电梯再上升10米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
(1)、求y与x的函数解析式(也称关系式),并直接写出自变量x的取值范围;(2)、如果6.5小时后该车还一直在上坡路上匀速行驶,问最多还能够行驶多少小时?20. 如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时该同学距地面的高度AE为27米,电梯再上升10米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号) 21. 为了落实“十九大报告﹣﹣乡村振兴战略”.某地方政府出台了一系列惠农政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克60元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣20x+1800.设这种产品每天的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、若规定该农产品销售单价不低于76元,且要完成每天不少于240千克的销售任务,则每天销售该农产品获得的最大利润是多少元?22. 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,AD与⊙O相切于点A,交BC的延长线于点D,点E是劣弧BC的中点,连接AE,CE.
21. 为了落实“十九大报告﹣﹣乡村振兴战略”.某地方政府出台了一系列惠农政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克60元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣20x+1800.设这种产品每天的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、若规定该农产品销售单价不低于76元,且要完成每天不少于240千克的销售任务,则每天销售该农产品获得的最大利润是多少元?22. 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,AD与⊙O相切于点A,交BC的延长线于点D,点E是劣弧BC的中点,连接AE,CE. (1)、求证:∠DAC=∠AEC;(2)、延长CE,AB交于点G,使得GB= AB,若AC=2,求⊙O的半径.23. 已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC,AC.
(1)、求证:∠DAC=∠AEC;(2)、延长CE,AB交于点G,使得GB= AB,若AC=2,求⊙O的半径.23. 已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC,AC. (1)、如图1,若点P在线段AB的延长线上,判断△ACE的形状,并说明理由;(2)、如图2,若点P在线段AB上
(1)、如图1,若点P在线段AB的延长线上,判断△ACE的形状,并说明理由;(2)、如图2,若点P在线段AB上①若点P是线段AB的中点,判断△ACE的形状,并说明理由;
②当 时,请直接写出∠CAE的度数.