云南省昆明市2020年数学中考三模试卷
试卷更新日期:2020-09-16 类型:中考模拟
一、填空题
-
1. 的倒数的绝对值是 .2. 2017年5月18日,我国宣布在南海神狐海域成功试采可燃冰,成为世界上首个在海域连续稳定产气的国家据粗略估计,仅南海北部陆坡的可燃冰资源就达到 亿吨油的量,达到我国陆上石油资源总量的 .数据 亿用科学记数法可表示为.3. 一元二次方程2x2-5x-2=0的根的情况是.4. 时, 的值为.5. 如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画 , 若 ,则阴影部分图形的周长为 结果保留 .
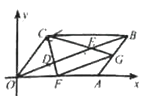
 6. 如图,平面直角坐标系中 是原点, 的顶点 的坐标分别是 ,点 把线段 三等分,延长 分别交 于点 ,连接 ,则下列结论:
6. 如图,平面直角坐标系中 是原点, 的顶点 的坐标分别是 ,点 把线段 三等分,延长 分别交 于点 ,连接 ,则下列结论:① 是 的中点;② 与 相似;③四边形 的面积是 ;④ ;其中正确的结论是 . (填写所有正确结论的序号)
二、单选题
-
7. 式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、8. 要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )A、288° B、144° C、216° D、120°9. 下列命题正确的是( )A、点 关于 轴的对称点是 B、函数 中, 随 的增大而增大 C、若一组数据 , , , , 的众数是 ,则中位数是 D、同圆中的两条平行弦所夹的弧相等10. 如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 11. 如图,在 中, , , 是 的两条中线, 是 上个动点,则下列线段的长度等于 最小值的是( )
11. 如图,在 中, , , 是 的两条中线, 是 上个动点,则下列线段的长度等于 最小值的是( )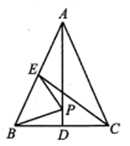 A、BC B、CE C、AD D、AC12. 已知抛物线 与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,则平移后的抛物线解析式为( )A、 B、 C、 D、13. 如图,已知直线l1:y=﹣2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(﹣2,0),则k的取值范围是( )
A、BC B、CE C、AD D、AC12. 已知抛物线 与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,则平移后的抛物线解析式为( )A、 B、 C、 D、13. 如图,已知直线l1:y=﹣2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(﹣2,0),则k的取值范围是( )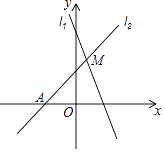 A、﹣2<k<2 B、﹣2<k<0 C、0<k<4 D、0<k<214. 如图,正方形ABCD中, ,点E是对角线AC上一点,连接BE,过点E作 ,交AB于点F,连接DF,交AC于点G,将 沿EF翻折,得到 ,连接DM,交EF于点N,若点F是AB的中点,则 的周长是( )
A、﹣2<k<2 B、﹣2<k<0 C、0<k<4 D、0<k<214. 如图,正方形ABCD中, ,点E是对角线AC上一点,连接BE,过点E作 ,交AB于点F,连接DF,交AC于点G,将 沿EF翻折,得到 ,连接DM,交EF于点N,若点F是AB的中点,则 的周长是( ) A、 B、 C、 D、
A、 B、 C、 D、三、计算题。
-
15. 计算:
四、解答题。
-
16. 小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°= + =1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)、当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;(2)、小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.17. 为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.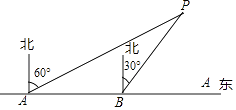 (1)、求∠APB的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?18. 某商店在 年至 年期问销售一种礼盒, 年该商店川 万元购进了这种礼盒并且全部售完. 年这种礼盒的进价比 年下降了 元/盒,该商店用 万元购进了与 年相同数量的礼盒也全部售完,礼盒的售价均为 元/盒(1)、 年这种礼盒的进价是多少元/盒?(2)、若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?19. 随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图,根据以下信息解答下列问题:
(1)、求∠APB的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?18. 某商店在 年至 年期问销售一种礼盒, 年该商店川 万元购进了这种礼盒并且全部售完. 年这种礼盒的进价比 年下降了 元/盒,该商店用 万元购进了与 年相同数量的礼盒也全部售完,礼盒的售价均为 元/盒(1)、 年这种礼盒的进价是多少元/盒?(2)、若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?19. 随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图,根据以下信息解答下列问题: (1)、2017年“五•一”期间,该市周边景点共接待游客万人,扇形统计图中A景点所对应的圆心角的度数是 , 并补全条形统计图.(2)、根据近几年到该市旅游人数增长趋势,预计2018年“五•一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.20. 如图 ,将一张矩形纸片 沿着对角线 向上折叠,顶点 落到点 处, 交 于点
(1)、2017年“五•一”期间,该市周边景点共接待游客万人,扇形统计图中A景点所对应的圆心角的度数是 , 并补全条形统计图.(2)、根据近几年到该市旅游人数增长趋势,预计2018年“五•一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?(3)、甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.20. 如图 ,将一张矩形纸片 沿着对角线 向上折叠,顶点 落到点 处, 交 于点 (1)、求证: 是等腰三角形;(2)、如图 ,过点 作 ,交 于点 ,连接 交 于点
(1)、求证: 是等腰三角形;(2)、如图 ,过点 作 ,交 于点 ,连接 交 于点①判断四边形 的形状,并说明理由;
②若 , ,求 的长
21. 宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y= .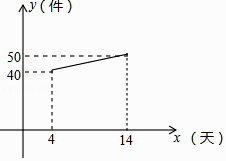 (1)、工人甲第几天生产的产品数量为70件?(2)、设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?22. 如图,直线 与 轴、 轴分别交于点 , ,经过 , 两点的抛物线 与 轴的负半轴的另一交点为 ,且
(1)、工人甲第几天生产的产品数量为70件?(2)、设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?22. 如图,直线 与 轴、 轴分别交于点 , ,经过 , 两点的抛物线 与 轴的负半轴的另一交点为 ,且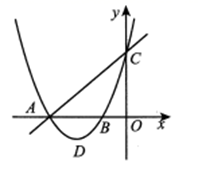 (1)、求该抛物线的解析式及抛物线顶点 的坐标;(2)、点 是射线 上一点,问是否存在以点 , , 为顶点的三角形,与 相似,若存在,请求出点 的坐标;若不存在,请说明理由23. 已知:AB是⊙O的弦,点C是 的中点,连接OB、OC,OC交AB于点D.
(1)、求该抛物线的解析式及抛物线顶点 的坐标;(2)、点 是射线 上一点,问是否存在以点 , , 为顶点的三角形,与 相似,若存在,请求出点 的坐标;若不存在,请说明理由23. 已知:AB是⊙O的弦,点C是 的中点,连接OB、OC,OC交AB于点D. (1)、如图1,求证:AD=BD;(2)、如图2,过点B作⊙O的切线交OC的延长线于点M,点P是 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;(3)、如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO= ,求 的值.
(1)、如图1,求证:AD=BD;(2)、如图2,过点B作⊙O的切线交OC的延长线于点M,点P是 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;(3)、如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO= ,求 的值.
-