云南省昆明市2020年数学中考二模试卷
试卷更新日期:2020-09-16 类型:中考模拟
一、填空题
-
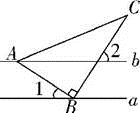
1. 分解因式: =2. 如图,直线 , 的直角顶点 落在直线 上,若 ,则 的大小为
 3. 如图,菱形ABCD的面积为120cm2 , 正方形AECF的面积为50cm2 , 则菱形的边长为cm.
3. 如图,菱形ABCD的面积为120cm2 , 正方形AECF的面积为50cm2 , 则菱形的边长为cm. 4. 如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .
4. 如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .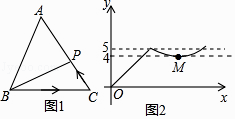 5. 设△ABC的面积为1,如图①,将边BC、AC分别2等分,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等分,BE1、AD1相交于点O,△AOB的面积记为S2;…,依此类推,则Sn可表示为 .(用含n的代数式表示,其中n为正整数)
5. 设△ABC的面积为1,如图①,将边BC、AC分别2等分,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等分,BE1、AD1相交于点O,△AOB的面积记为S2;…,依此类推,则Sn可表示为 .(用含n的代数式表示,其中n为正整数)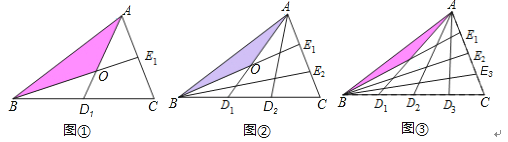 6. 如图,在 中, , , ,点 , 分别是边 , 上的动点,沿 所在的直线折叠 ,使点 的对应点 始终落在边 上,若 为直角三角形,则 的长为.
6. 如图,在 中, , , ,点 , 分别是边 , 上的动点,沿 所在的直线折叠 ,使点 的对应点 始终落在边 上,若 为直角三角形,则 的长为.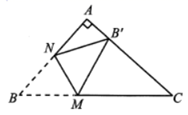
二、单选题
-
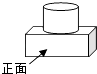
7. 下列计算正确的是( )A、 B、 C、 D、8. 如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
 A、
A、 B、
B、 C、
C、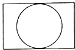 D、
D、 9. 为缓解中低收入人群和新参加工作的大学生住房的需求,某市将新建保障住房3600000套,把3600000用科学记数法表示应是( )A、0.36×107 B、3.6×106 C、3.6×107 D、36×10510. 要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
9. 为缓解中低收入人群和新参加工作的大学生住房的需求,某市将新建保障住房3600000套,把3600000用科学记数法表示应是( )A、0.36×107 B、3.6×106 C、3.6×107 D、36×10510. 要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A、平均数 B、中位数 C、众数 D、方差11. 如图,在任意四边形 中, , , , 分别是 , , , 上的点,对于四边形 的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( ) A、当 , , , 是各边中点,且 时,四边形 为菱形 B、当 , , , 是各边中点,且 时,四边形 为矩形 C、当 , , , 不是各边中点时,四边形 可以为平行四边形 D、当 , , , 不是各边中点时,四边形 不可能为菱形12. 如图,已知 三个顶点的坐标分别为 , , .将 向右平移 个单位,得到 ,点 , , 的对应点分别为 , , ,再将 绕点 顺时针旋转 ,得到 ,点 , , 的对应点分别为 , , ,则点 的坐标为( )
A、当 , , , 是各边中点,且 时,四边形 为菱形 B、当 , , , 是各边中点,且 时,四边形 为矩形 C、当 , , , 不是各边中点时,四边形 可以为平行四边形 D、当 , , , 不是各边中点时,四边形 不可能为菱形12. 如图,已知 三个顶点的坐标分别为 , , .将 向右平移 个单位,得到 ,点 , , 的对应点分别为 , , ,再将 绕点 顺时针旋转 ,得到 ,点 , , 的对应点分别为 , , ,则点 的坐标为( )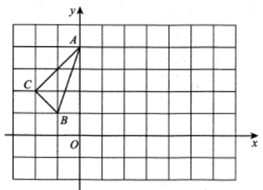 A、 B、 C、 D、13. 如图,将半径为 ,圆心角为120°的扇形 绕点 逆时针旋转60°,点 , 的对应点分别为 , ,连接 ,则图中阴影部分的面积是( )
A、 B、 C、 D、13. 如图,将半径为 ,圆心角为120°的扇形 绕点 逆时针旋转60°,点 , 的对应点分别为 , ,连接 ,则图中阴影部分的面积是( ) A、 B、 C、 D、14.
A、 B、 C、 D、14.下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )
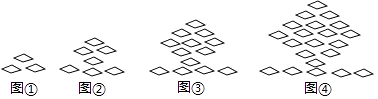 A、73 B、81 C、91 D、109
A、73 B、81 C、91 D、109三、解答题
-
15. 下面小题选做一题。(1)、计算: .(2)、先化简,再求值: ,其中 , 满足16. (1)、(2)题选做一题.(1)、在等边 中,点 , 分别在边 , 上,若 ,过点 作 ,过点 作 ,交 的延长线于点 .求 的长.
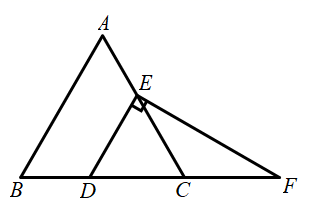 (2)、如图,在正方形 中, , 分别为边 和 上的点,且 ,连接 , 交于点 .
(2)、如图,在正方形 中, , 分别为边 和 上的点,且 ,连接 , 交于点 .
求证: .
17. 如图,直线y=k1x(x≥0)与双曲线y= (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP. (1)、求k1与k2的值;(2)、求直线PC的解析式;(3)、直接写出线段AB扫过的面积.18. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
(1)、求k1与k2的值;(2)、求直线PC的解析式;(3)、直接写出线段AB扫过的面积.18. 为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.调查结果统计表
组别
分组(单位:元)
人数
调查结果扇形统计图
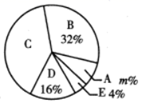
请根据以上图表,解答下列问题:
(1)、这次被调查的同学共有人, , ;(2)、求扇形统计图中扇形 的圆心角度数;(3)、该校共有 人,请估计每月零花钱的数额 在 范围的人数.19. 某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间 (单位:小时),将学生分成五类: 类( ), 类( ), 类( ), 类( ), 类( ),绘制成尚不完整的条形统计图如图11.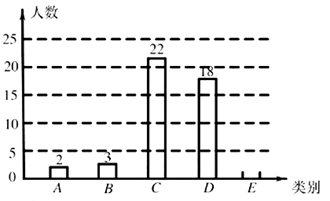
根据以上信息,解答下列问题:
(1)、 类学生有人,补全条形统计图;(2)、 类学生人数占被调查总人数的%;(3)、从该班做义工时间在 的学生中任选2人,求这2人做义工时间都在 中的概率.20. 如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)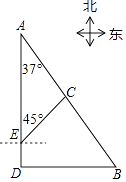 21. 自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16 000元采购A型商品的件数是用7 500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A,B型商品的进价分别为多少元?(2)、若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数解析式,并写出m的取值范围;(3)、在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.22. 如图, 是 的直径,点 是 上一点, 和过点 的切线互相垂直,垂足为点 ,直线 与 的延长线相交于点 .弦 平分 ,交直径 于点 ,连接 .
21. 自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16 000元采购A型商品的件数是用7 500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.(1)、求一件A,B型商品的进价分别为多少元?(2)、若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数解析式,并写出m的取值范围;(3)、在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.22. 如图, 是 的直径,点 是 上一点, 和过点 的切线互相垂直,垂足为点 ,直线 与 的延长线相交于点 .弦 平分 ,交直径 于点 ,连接 .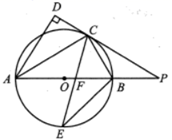 (1)、求证: 平分 ;(2)、探究线段 , 之间的大小关系,并加以证明;(3)、若 , ,求 的长.23. 如图,在平面直角坐标系中,点 为坐标原点,抛物线 交 轴于 , 两点,交 轴于点 ,直线 经过 , 两点.
(1)、求证: 平分 ;(2)、探究线段 , 之间的大小关系,并加以证明;(3)、若 , ,求 的长.23. 如图,在平面直角坐标系中,点 为坐标原点,抛物线 交 轴于 , 两点,交 轴于点 ,直线 经过 , 两点. (1)、求抛物线的解析式;(2)、过点 作直线 轴交抛物线于另一点 ,点 是直线 下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点 作 轴于点 , 交 于点 ,交 于点 ,连接 ,过点 作 于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 之间的函数解析式(不要求写出自变量 的取值范围);(3)、在(2)的条件下,连接 ,过点 作 于点 (点 在线段 上), 交 于点 ,连接 交 于点 ,当 时,求线段 的长.
(1)、求抛物线的解析式;(2)、过点 作直线 轴交抛物线于另一点 ,点 是直线 下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点 作 轴于点 , 交 于点 ,交 于点 ,连接 ,过点 作 于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 之间的函数解析式(不要求写出自变量 的取值范围);(3)、在(2)的条件下,连接 ,过点 作 于点 (点 在线段 上), 交 于点 ,连接 交 于点 ,当 时,求线段 的长.