云南省红河州石屏县2020年数学中考一模试卷

试卷更新日期：2020-09-16 类型：中考模拟

进入 出卷网 下载

一、填空题。

  • 1. −12020 的倒数是.

    查看试题解析

  • 2. 云南，简称云或滇，位于中国西南边陲，是人类文明重要发祥地之一，有“彩云之南”、“七彩云南”之称，面积约394000平方千米，居全国第八.将数字394000用科学记数法表示为.

    查看试题解析

  • 3. 不等式组 {x−2<03x+5>0 的解集是.

    查看试题解析

  • 4. 如图，直线a∥b，直线c与直线a、b分别交于A、B两点，AC⊥b于点C，若∠1＝43°，则∠2＝.

    查看试题解析

  • 5. 已知（x﹣1）2＝2，则代数式2x2﹣4x+5＝.

    查看试题解析

  • 6. 如图，BD、CE是△ABC的角平分线，它们相交于点O，若∠A＝64°，则∠BOC＝.

    查看试题解析

二、单选题

  • 7. 函数y= x−1x−2 中，自变量x的取值范围是（   ）
    A、x≥1 B、x＞1 C、x≥1且x≠2 D、x≠2

    查看试题解析

  • 8. 下列计算正确是（   ）
    A、3﹣1＝﹣3 B、5−2=3 C、a6÷a2＝a4 D、（ −12 ）0＝0

    查看试题解析

  • 9.

    一个几何体的三视图如图所示，则这个几何体是（　　）


    A、球体 B、圆锥 C、棱柱 D、圆柱

    查看试题解析

  • 10. 某校九年级数学模拟测试中，六名学生的数学成绩如下表所示，下列关于这组数据描述正确的是（   ）

    姓名

    小红

    小明

    小东

    小亮

    小丽

    小华

    成绩（分）

    110

    106

    109

    111

    108

    110
    A、众数是110 B、方差是16 C、平均数是109.5 D、中位数是109

    查看试题解析

  • 11. 关于x的一元二次方程x2+3x﹣1＝0的根的情况是（    ）
    A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

    查看试题解析

  • 12. 一个扇形的圆心角为60°，它所对的弧长为2πcm，则这个扇形的半径为（       ）

    A、6cm B、12cm C、23cm D、6cm

    查看试题解析

  • 13. 如图，四边形OABC是矩形，等腰△ODE中，OE＝DE，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点B、E在反比例函数y＝ kx 的图象上，OA＝5，OC＝1，则△ODE的面积为（   ）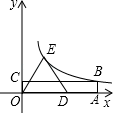

    A、2.5 B、5 C、7.5 D、10

    查看试题解析

  • 14. 如图，正方形ABCD的边长为1，顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1 ， 由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…，以此类推，则第六个正方形A6B6C6D6周长是（   ）

    A、12 B、13 C、14 D、15

    查看试题解析

三、解答题

  • 15. 计算：（﹣1）2020﹣ 8+(π−3)0 +4cos45°.

    查看试题解析

  • 16. 如图，∠B＝∠D，∠1＝∠2，AB＝AD.求证：BC＝DE.

    查看试题解析

  • 17. 某水果批发市场，香蕉和苹果某天的批发价与市场零售价如下表所示：

    水果经营户老王从水果批发市场批发香蕉与苹果用了470元，当天他卖完这些香蕉和苹果共赚了340元，这天他批发的香蕉和苹果分别是多少千克？

    查看试题解析

  • 18. 甲、乙两个袋中均有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标的数值分别为﹣7，﹣1，3，乙袋中的三张卡片上所标的数值分别为﹣2，1，6.先从甲袋中随机取出一张卡片，用x表示取出的卡片上标的数值，再从乙袋中随机取出一张卡片，用y表示取出的卡片上标的数值，把x、y分别作为点A的横坐标、纵坐标.
    (1)、用适当的方法写出点A（x，y）的所有情况；
    (2)、求点A落在第二象限的概率.

    查看试题解析

  • 19. 如图，某校数学兴趣小组的小明同学为测量位于玉溪大河畔的云铜矿业大厦AB的高度，小明在他家所在的公寓楼顶C处测得大厦顶部A处的仰角为45°，底部B处的俯角为30°.已知公寓高为40m，请你帮助小明计算公寓楼与矿业大厦间的水平距离BD的长度及矿业大厦AB的高度.（结果保留根号）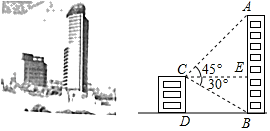

    查看试题解析

  • 20. 为挑选优秀同学参加云南省级英语听说能力竞赛，某中学举行了“英语单词听写”竞赛，每位学生听写单词99个，比赛结束后随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分.

    根据以上信息解决下列问题：

    (1)、本次共随机抽查了名学生，并补全频数分布直方图；
    (2)、若把每组听写正确的个数用这组数据的组中值代替，则被抽查学生听写正确的个数的平均数是多少？
    (3)、该校共有3000名学生，如果听写正确的个数少于60个定为不合格，请你估计这所学校本次竞赛听写不合格的学生人数.

    查看试题解析

  • 21. A粮仓和B粮仓分别库存粮食12吨和6吨，现决定支援给C市10吨和D市8吨．已知从A粮仓调运一吨粮食到C市和D市的运费分别为400元和800元；从B粮仓调运一吨粮食到C市和D市的运费分别为300元和500元．
    (1)、设B粮仓运往C市粮食x吨，求总运费W（元）关于x的函数关系式．（写出自变量的取值范围）
    (2)、若要求总运费不超过9000元，问共有几种调运方案？
    (3)、求出总运费最低的调运方案，最低运费是多少？

    查看试题解析

  • 22. 如图，在▱ABCD中，AE平分∠BAD交DC于点E，AD＝5cm，AB＝8cm.

    (1)、求EC的长.
    (2)、作∠BCD的平分线交AB于F，求证：四边形AECF为平行四边形.

    查看试题解析

  • 23. 在平面直角坐标系中，二次函数y＝ax2+bx+2的图象与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C.

    (1)、求这个二次函数的关系解析式；
    (2)、点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由；
    (3)、在平面直角坐标系中，是否存在点Q，使△BCQ是以BC为腰的等腰直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由；

    查看试题解析