云南省昆明市云大附中一二一校区2020年数学中考三模试卷
试卷更新日期:2020-09-16 类型:中考模拟
一、填空题。
-
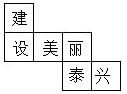
1. 的倒数是.2. 如图是正方体的表面展开图,则与“建”字相对的字是.
 3. 要使代数式 有意义,则x的取值范围是 .4. 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是cm.
3. 要使代数式 有意义,则x的取值范围是 .4. 如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是cm.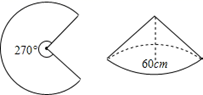 5. 如图,直线y=m与反比例函数y= 和y= 的图象分别交于A、B两点,点C是x轴上任意一点,则 ABC的面积为.
5. 如图,直线y=m与反比例函数y= 和y= 的图象分别交于A、B两点,点C是x轴上任意一点,则 ABC的面积为.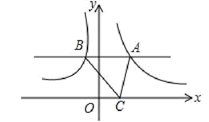 6. 矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数.
6. 矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数.
二、单选题。
-
7. 随着环境污染整治的逐步推进,某经济开发区的40家化工企业已关停、整改38家,每年排放的污水减少了167000吨.将167000用科学记数法表示为( )A、167´103 B、16.7´104 C、1.67´105 D、0.167´1068. 不等式组 的解集在数轴上表示正确的是( )A、
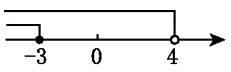 B、
B、 C、
C、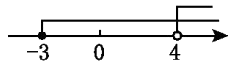 D、
D、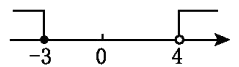 9. 下列运算正确的是( )A、a2+a3=a5 B、(﹣2a2)3=﹣6a6 C、(2a+1)(2a﹣1)=2a2﹣1 D、(2a3﹣a2)÷a2=2a﹣110. 下列说法正确的是( )A、“任意画一个六边形,它的内角和是720度”,这是一个随机事件 B、为了解全国中学生的心理健康情况,应该采用全面调查的方式 C、一组数据6,8,7,9,7,10的众数和中位数都是7 D、若甲组数据的方差S甲2=0.04,乙组数据的方差S乙2=0.05,为则甲组数据更稳定11. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
9. 下列运算正确的是( )A、a2+a3=a5 B、(﹣2a2)3=﹣6a6 C、(2a+1)(2a﹣1)=2a2﹣1 D、(2a3﹣a2)÷a2=2a﹣110. 下列说法正确的是( )A、“任意画一个六边形,它的内角和是720度”,这是一个随机事件 B、为了解全国中学生的心理健康情况,应该采用全面调查的方式 C、一组数据6,8,7,9,7,10的众数和中位数都是7 D、若甲组数据的方差S甲2=0.04,乙组数据的方差S乙2=0.05,为则甲组数据更稳定11. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( ) A、9 B、6 C、4 D、312. a,b,c为常数,且 ,则关于x的方程 根的情况是A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为013. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A、9 B、6 C、4 D、312. a,b,c为常数,且 ,则关于x的方程 根的情况是A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为013. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )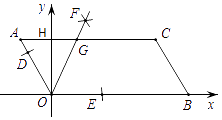 A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)14.
A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)14.如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )
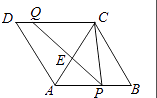 A、5 B、7 C、8 D、
A、5 B、7 C、8 D、三、解答题。
-
15.
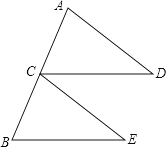
已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
 16. 如下:(1)、计算:(2)、先化简,再求值: ,其中17. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球,B.乒乓球,C.羽毛球,D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图.请回答下列问题:
16. 如下:(1)、计算:(2)、先化简,再求值: ,其中17. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球,B.乒乓球,C.羽毛球,D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图.请回答下列问题: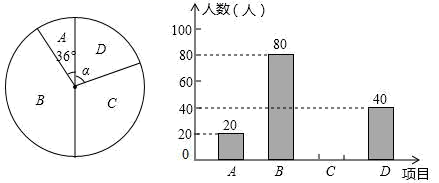 (1)、这次被调查的学生共有人,扇形统计图中B部分所对应扇形的圆心角为度(2)、请你将条形统计图2补充完整:(3)、如果该校共有学生1200人,估计全校喜欢足球的学生有多少人?(4)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率.(用树状图或列表法解答)18.
(1)、这次被调查的学生共有人,扇形统计图中B部分所对应扇形的圆心角为度(2)、请你将条形统计图2补充完整:(3)、如果该校共有学生1200人,估计全校喜欢足球的学生有多少人?(4)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率.(用树状图或列表法解答)18.如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
 19. 李华从文化宫站出发,先乘坐地铁,准备在离家较近的A、B、C、D中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
19. 李华从文化宫站出发,先乘坐地铁,准备在离家较近的A、B、C、D中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:地铁站
A
B
C
D
E
x(千米)
8
9
10
11.5
13
Y1(分钟)
18
20
22
25
28
(1)、求y1关于x的函数表达式;(2)、李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用 来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家里所需的时间最短?并求出最短时间.20. 某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2017年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可提前4年完成任务.(1)、问实际每年绿化面积多少万平方米?(2)、为加大创文力度,市政府决定从2020年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?21. 如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG^AC,垂足为E,DG分别与AB及CB延长线交于点F、M.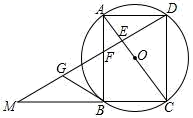 (1)、求证:四边形ABCD是矩形;(2)、若点G为MF的中点,求证:BG是⊙O的切线;22. 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B,与y轴交于点C
(1)、求证:四边形ABCD是矩形;(2)、若点G为MF的中点,求证:BG是⊙O的切线;22. 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B,与y轴交于点C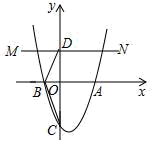 (1)、求点A,B的坐标;(2)、过点D(0,3)作直线MN∥x轴,点P在直线MN上,且 ,直接写出点P的坐标.23. 爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)、求点A,B的坐标;(2)、过点D(0,3)作直线MN∥x轴,点P在直线MN上,且 ,直接写出点P的坐标.23. 爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.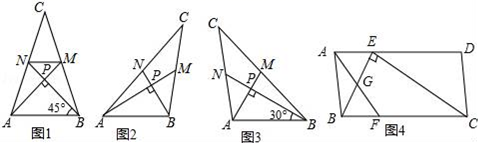 (1)、(特例探究)
(1)、(特例探究)如图1,当tan∠PAB=1,c=4 时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)、(归纳证明)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)、(拓展证明)如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ,AB=3,求AF的长.