天津市和平区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则x的取值范围是( )A、x<3 B、x≤3 C、x>3 D、x≥32. 有下列算式:(1) ;(2) ;(3) ;(4) ;其中正确的是( )A、(2)和(4) B、(1)和(3) C、(3)和(4) D、(1)和(4)3. 如图,在矩形 中,对角线 , 交于点 ,以下说法错误的是( )
 A、 B、 C、 D、4. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 某个一次函数的图象与直线 平行,并且经过点 ,则这个一次函数的解析式为( )A、 B、 C、 D、6. 利用勾股定理,可以作出长为无理数的线段.如图,在数轴上找到点 ,使 ,过点 作直线 垂直于 ,在 上取点 ,使 ,以原点 为圆心,以 长为半径作弧,弧与数轴的交点为 ,那么点 表示的无理数是( )
A、 B、 C、 D、4. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 某个一次函数的图象与直线 平行,并且经过点 ,则这个一次函数的解析式为( )A、 B、 C、 D、6. 利用勾股定理,可以作出长为无理数的线段.如图,在数轴上找到点 ,使 ,过点 作直线 垂直于 ,在 上取点 ,使 ,以原点 为圆心,以 长为半径作弧,弧与数轴的交点为 ,那么点 表示的无理数是( )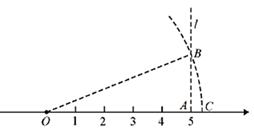 A、 B、 C、7 D、7. 某招聘考试要进行笔试和面试,其中笔试占60%,面试占40%.孔明笔试成绩90分,面试成绩85分,那么孔明的最后成绩是( )A、88.5分 B、88分 C、87.5分 D、87分8. 顺次连接菱形各边的中点所形成的四边形是( )A、等腰梯形 B、矩形 C、菱形 D、正方形9. 下列命题中,是真命题的是()A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形10. 已知一次函数 的图象如图所示,当 时,y的取值范围是
A、 B、 C、7 D、7. 某招聘考试要进行笔试和面试,其中笔试占60%,面试占40%.孔明笔试成绩90分,面试成绩85分,那么孔明的最后成绩是( )A、88.5分 B、88分 C、87.5分 D、87分8. 顺次连接菱形各边的中点所形成的四边形是( )A、等腰梯形 B、矩形 C、菱形 D、正方形9. 下列命题中,是真命题的是()A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形10. 已知一次函数 的图象如图所示,当 时,y的取值范围是 A、 B、 C、 D、11. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 与甲车行驶的时间 之间的函数关系如图所示.下列说法错误的是( )
A、 B、 C、 D、11. 甲、乙两车从 城出发匀速行驶至 城,在整个行驶过程中,甲、乙两车离开 城的距离 与甲车行驶的时间 之间的函数关系如图所示.下列说法错误的是( )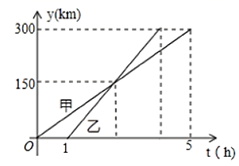 A、 , 两城相距 千米 B、乙车比甲车晚出发 小时,却早到 小时 C、乙车出发后 小时追上甲车 D、在一车追上另一车之前,当两车相距 千米时,12. 如图1,将正方形 置于平面直角坐标系中,其中 边在 轴上,其余各边均与坐标轴平行.直线 沿 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形 的边所截得的线段长为 ,平移的时间为 (秒), 与 的函数图象如图2所示,则图2中 的值为( )
A、 , 两城相距 千米 B、乙车比甲车晚出发 小时,却早到 小时 C、乙车出发后 小时追上甲车 D、在一车追上另一车之前,当两车相距 千米时,12. 如图1,将正方形 置于平面直角坐标系中,其中 边在 轴上,其余各边均与坐标轴平行.直线 沿 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形 的边所截得的线段长为 ,平移的时间为 (秒), 与 的函数图象如图2所示,则图2中 的值为( )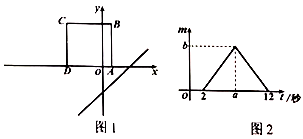 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算 的结果等于 .14. 某班随机调查了10名学生,了解他们一周的体育锻炼时间,结果如下表所示:
时间(小时)
7
8
9
人数
3
4
3
则这10名学生在这一周的平均体育锻炼时间是小时.
15. 某次射击练习,甲、乙二人各射靶 次,命中的环数如下表:甲射靶环数
乙射靶环数
通过计算可知 , , ,所以射击成绩比较稳定的是 .
16. 若正比例函数y=kx(k为常数,且k≠0)的函数值y随着x的增大而减小,则k的值可以是 . (写出一个即可)17. 已知一次函数 ,当 时,函数 的最大值是 .18. 如图,在 中, , 为 边上的中线,过点 作 于点 ,过点 作 的平行线,交 的延长线于点 ,在 的延长线上截取 ,连接 、 .若 , ,则 的长为 .
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:
 (1)、本次抽测的男生人数为 , 图①中m的值为;(2)、求本次抽测的这组数据的平均数、众数和中位数;(3)、若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.21. 如图, 是一个边长为 的等边三角形, 是 的高,求 的长.
(1)、本次抽测的男生人数为 , 图①中m的值为;(2)、求本次抽测的这组数据的平均数、众数和中位数;(3)、若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.21. 如图, 是一个边长为 的等边三角形, 是 的高,求 的长. 22. 已知,四边形 是菱形,
22. 已知,四边形 是菱形, (1)、若 ,则菱形 的周长 ;(2)、如图①, , 是对角线,则 与 的位置关系是;(3)、如图②,点 , 分别在 , 上,且 , , ,点 , 分别在 , 上, 与 相交于点 .
(1)、若 ,则菱形 的周长 ;(2)、如图①, , 是对角线,则 与 的位置关系是;(3)、如图②,点 , 分别在 , 上,且 , , ,点 , 分别在 , 上, 与 相交于点 .求证:四边形 是菱形.
23. 甲、乙两家商场平时以同样价格出售相同的商品春节期间两家商场都让利酬宾,其中甲商场所有商品按 折出售,乙商场对一次购物中超过 元后的价格部分打 折.设原价购物金额累计为 元 .
(1)、根据题意,填写下表:原价购物金额累计 元
130
300
500
700
甲商场实际购物金额 元
104
560
乙商场实际购物金额 元
130
270
(2)、设在甲商场实际购物金额为 元,在乙商场实际购物金额为 元,分别写出 , 关于x的函数解析式;(3)、根据题意填空:①若在甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为元;
②若在同一商场购物,商品原价购物金额累计为 元,则在甲、乙两家商场中的商场实际购物花费金额少;
③若在同一商场实际购物金额为 元,则在甲、乙两家商场中的商场商品原价购物累计金额多


