上海市嘉定区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 一次函数 $y = - 3 x - 2$ 的截距是（）

A、-3 B、-2 C、2 D、3

查看试题解析
2. 如果关于 $x$ 的方程 $(a - 3) x = 2020$ 的解为负数，那么实数 $a$ 的取值范围是（）

A、 $a < 3$ B、 $a = 3$ C、 $a > 3$ D、 $a \neq 3$

查看试题解析
3. 下列方程中，有实数根的是（）

A、 $x^{4} + 1 = 0$ B、 $\sqrt{x - 2} + 1 = 0$ C、 $\sqrt{x + 2} = - x$ D、 $\frac{x}{x^{2} - 1} = \frac{1}{x^{2} - 1}$

查看试题解析
4. 将只有颜色不同的3个白球、2个黑球放在一个不透明的布袋中.下列四个选项，错误的是（）

A、摸到白球比摸到黑球的可能性大 B、摸到白球和黑球的可能性相等 C、摸到红球是确定事件 D、摸到黑球或白球是确定事件

查看试题解析
5. 下列四个命题中，假命题是（）

A、有两个内角相等的梯形是等腰梯形 B、等腰梯形一定有两个内角相等 C、两条对角线相等的梯形是等腰梯形 D、等腰梯形的两条对角线相等

查看试题解析
6. 已知四边形 $A B C D$ 是矩形，点 $O$ 是对角线 $A C$ 与 $B D$ 的交点.下列四种说法：①向量 $\vec{A O}$ 与向量 $\vec{O C}$ 是相等的向量；②向量 $\vec{O A}$ 与向量 $\vec{O C}$ 是互为相反的向量；③向量 $\vec{A B}$ 与向量 $\vec{C D}$ 是相等的向量；④向量 $\vec{B O}$ 与向量 $\vec{B D}$ 是平行向量．其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 已知一次函数 $f (x) = 3 x + 2$ ，那么 $f (- 1) =$ ．

查看试题解析
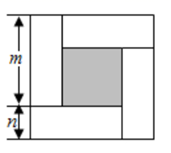
8. 如果将直线 $y = \frac{1}{2} x$ 沿 $y$ 轴向下平移2个单位，那么平移后所得直线的表达式是．

查看试题解析
9. 已知函数 $y = - 3 x + 7$ ，当 $y < 1$ 时，自变量 $x$ 的取值范围是．

查看试题解析
10. 二项方程 $2 x^{3} + 16 = 0$ 在实数范围内的解是．

查看试题解析
11. 用换元法解方程 $\frac{x}{x^{2} - 1} + \frac{3 (x^{2} - 1)}{x} = 4$ ，若设 $\frac{x}{x^{2} - 1} = y$ ，那么所得到的关于 $y$ 的整式方程为．

查看试题解析
12. 某校八年级在“停课不停学”期间，积极开展网上答疑活动．在某时间段共开放7个网络教室，其中1个是语文答疑教室，3个是数学答疑教室，3个是英语答疑教室.为了解学校的八年级学生参与网上答疑的情况，学校教学管理人员随机进入一个网络教室，那么他进入数学答疑教室的概率为．

查看试题解析
13. 已知一个梯形的中位线长为5 $c m$ ，其中一条底边的长为6 $c m$ ，那么该梯形的另一条底边的长是 $c m$ ．

查看试题解析
14. 已知菱形的边长为2cm，一个内角为 $60 °$ ，那么该菱形的面积为cm² ．

查看试题解析
15. 已知梯形的两底长分别为2和8，两腰的长分别为4与 $a$ ，那么字母 $a$ 的取值范围为．

查看试题解析
16. 已知四边形 $A B C D$ ，点 $O$ 是对角线 $A C$ 与 $B D$ 的交点，且 $O A = O C$ ，请再添加一个条件，使得四边形 $A B C D$ 成为平行四边形，那么添加的条件可以是．（用数学符号语言表达）

查看试题解析
17. 贾老师用四个大小、形状完全相同的小长方形围成了一个大正方形，如果大正方形的面积为3，且 $m = 3 n$ 那么图中阴影部分的面积是．

查看试题解析

三、解答题

18. 解方程： $\frac{x + 1}{x - 1} - \frac{2}{x^{2} - 1} = \frac{1}{x + 1}$

查看试题解析
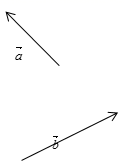
19. 解方程组： ${\begin{array}{l} x - y = 2 ， \\ x^{2} - 2 x y - 3 y^{2} = 0. \end{array}$

查看试题解析
20. 如图，已知向量 $\vec{a}$ 、 $\vec{b}$ ，用直尺与圆规先作向量 $\vec{a} + \vec{b}$ ，再作向量 $\vec{a} - \vec{b}$ ．（不写画法，保留画图痕迹，并在答案中注明所求作的向量．

查看试题解析
21. 某市为了美化环境，计划在一定的时间内完成绿化面积 $200$ 万亩的任务，后来市政府调整了原定计划，不但绿化面积要在原计划的基础上增加 $20 %$ ，而且要提前 $1$ 年完成任务，经测算要完成新的计划，平均每年的绿化面积必须比原计划多 $20$ 万亩，求原计划平均每年的绿化面积．

查看试题解析
22. 已知平行四边形 $A B C D$ ，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，且 $C A = C B$ ，延长 $B C$ 至点 $E$ ，使 $C E = B C$ ，联结 $D E$ ．

(1)、当 $A C ⊥ B D$ 时，求证： $B E = 2 C D$ ；

(2)、当 $∠ A C B = 90 °$ 时，求证：四边形 $A C E D$ 是正方形．

查看试题解析
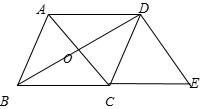23. 在平面直角坐标系 $x O y$ 中，已知一次函数 $y = - \frac{4}{3} x + b$ 的图像与 $x$ 轴、 $y$ 轴分别相交于点 $A$ 、 $B$ ，且与两坐标轴所围成的三角形的面积为6．

(1)、直接写出点 $A$ 与点 $B$ 的坐标（用含 $b$ 的代数式表示）；

(2)、求 $b$ 的值；

(3)、如果一次函数 $y = - \frac{4}{3} x + b$ 的图像经过第二、三、四象限，点C的坐标为（2，m），其中 $m > 0$ ，试用含 $m$ 的代数式表示△ $A B C$ 的面积．

查看试题解析
24. 已知四边形ABCD是正方形，将线段CD绕点C逆时针旋转 $α$ （ $0 ° < α < 90 °$ ），得到线段CE，联结BE、CE、DE. 过点B作BF⊥DE交线段DE的延长线于F．

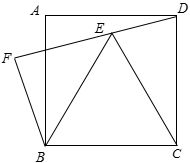(1)、如图，当BE=CE时，求旋转角 $α$ 的度数；

(2)、当旋转角 $α$ 的大小发生变化时， $∠ B E F$ 的度数是否发生变化?如果变化，请用含 $α$ 的代数式表示；如果不变，请求出 $∠ B E F$ 的度数；

(3)、联结AF，求证： $D E = \sqrt{2} A F$ ．

查看试题解析