山西省吕梁市文水县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{3}$ C、 $\sqrt{0.01}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 已知△ABC的三边分别为a、b、c，下列条件中，不能判定△ABC为直角三角形的是（）

A、 $∠ A = ∠ B + ∠ C$ B、 $a ： b ： c = 1 ： 1 ： \sqrt{2}$ C、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ D、 $b^{2} = a^{2} + c^{2}$

查看试题解析
3. 若点P在一次函数 $y = - x + 3$ 的图象上，则点P一定不在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$ B、 $\sqrt{3} + \sqrt{27} = 4 \sqrt{3}$ C、 $\sqrt{{(- 5)}^{2}} = - 5$ D、 $4 \sqrt{2} \div 2 \sqrt{2} = 2 \sqrt{2}$

查看试题解析
5. 疫情期间，小颖宅家学习．一天，她在课间休息时，从窗户向外望，看到一人为快速从A处到达居住楼B处，直接从边长为24米的正方形草地中穿过．为保护草地，小颖计划在A处立一个标牌：“少走？米，踏之何忍”，已知B、C两处的距离为7米，那么标牌上？处的数字是（）

A、3 B、4 C、5 D、6

查看试题解析
6. 学习了平行四边形的相关知识后，小明采用下列方法钉制了一个平行四边形框架：如图，将两根木条AC、BD的中点重叠并用钉子固定，然后用木条将AB、BC、CD、DA分别钉起来．此时四边形ABCD即为平行四边形，这样做的依据是（）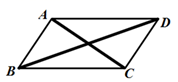

A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形

查看试题解析
7. 下表记录了甲、乙、丙、丁四位跳远运动员选拔赛成绩的平均数与方差：

根据表中信息，请你选择一名成绩好且发挥稳定的选手参赛，最合适的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如图，在Rt△ABC中，∠A＝90°，D，E分别是AB，BC的中点，点F在DE的延长线上，连接CF，请添加一个条件使四边形ADFC为矩形，则这个条件是（）

A、AC＝CF B、AD＝CF C、∠B＝∠BCF D、DB＝CF

查看试题解析
9. 一列快车从甲地驶往乙地，一列特快车从乙地驶往甲地，快车的速度为100千米/时，特快车的速度为150千米/时，甲乙两地相距1500千米，两车同时出发，则图中折线可以表示两车之间的距离y（千米）与快车行驶时间t（小时）之间函数关系的图象的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，若AD＝2AB，则下列结论错误的是（）

A、四边形EFGH为菱形 B、S_四边形_ABCD＝2S_四边形_EFGH C、 $E F = \frac{\sqrt{3}}{2} A B$ D、 $E F = \frac{\sqrt{5}}{2} A B$

查看试题解析

二、填空题

11. 等式 $\sqrt{\frac{7 - x}{x + 2}} = \frac{\sqrt{7 - x}}{\sqrt{x + 2}}$ 成立的条件是．

查看试题解析
12. 如图，已知菱形ABCD中，∠BAD＝120°，对角线AC与BD相交于点O，且AC＝ $2 \sqrt{3}$ ，则对角线BD的长为．

查看试题解析
13. 如图，一次函数 $y = a x + b$ 与正比例函数 $y = k x$ 的图象交于点P（－2，－1），则关于 $x$ 的方程 $a x + b = k x$ 的解是．

查看试题解析
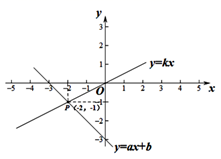14. 如图，是矗立在高速公路地面上的一块交通警示牌，经测量得知PA＝4米，AB＝5米，∠PAD＝45°，∠PBC＝30°，则警示牌的高CD为． (结果保留小数点后一位）

查看试题解析
15. 如图，在菱形ABCD中，按如下步骤作图：①分别以点C和点D为圆心，大于 $\frac{1}{2} C D$ 长为半径作弧，两弧交于点M、N；②作直线MN，且MN恰好经过点A，与CD交于点E，连接BE，若AD＝6，则BE的长为．

查看试题解析

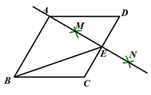
三、解答题

16. 计算

(1)、 $\sqrt{12} - 4 \sqrt{15} \div \sqrt{5} + 3 \sqrt{\frac{1}{3}}$

(2)、 $(\sqrt{3} - 2) (\sqrt{3} + 2) - (- \sqrt{8}) + | 1 - \sqrt{2} |$

查看试题解析
17. 已知 $x = \sqrt{5} + 2, y = \sqrt{5} - 2$ ，求 $x^{2} + x y + y^{2}$ 的值．

查看试题解析
18. 如图，在平面直角坐标系中，点A（6，n）为直线 $y = \frac{4}{3} x$ 上一点，以OA为边作菱形OABC，点C在 $x$ 轴上，直线AC的解析式为 $y = k x + b$ ．

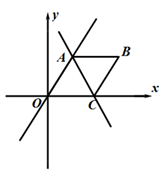(1)、求出n的值；

(2)、求直线AC的解析式；

(3)、根据图象，写出 $k x + b < \frac{4}{3} x$ 的解集．

查看试题解析
19. 随着防溺水安全教育活动的深入开展，学生安全防范意识不断增强．近日，某校从八年级随机抽取了50名学生，针对防溺水相关知识进行了测试，并将成绩（百分制）整理、描述和分析，部分信息如下：
a：成绩频数分布直方图：

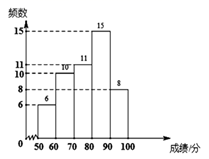
b：成绩在 $70 \leq x < 80$ 这一组的是：70 72 73 75 75 76 77 77 78 79 79

根据以上信息，回答下列问题：

(1)、在这次测试中，成绩在80分（含80分）以上的有名．

(2)、这50名学生的成绩的中位数是．

(3)、该校八年级学生有1100名，若全部参加此项测试，请估计成绩在70分以上（含70分）的学生约有多少名？

查看试题解析
20. 如图，在菱形ABCD中，对角线AC、BD相交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF，已知BF＝8，DF＝4，求CD的长．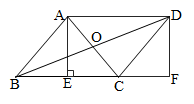

查看试题解析
21. 为了加强环境保护，进一步提升污水处理能力，我县某污水处理厂决定购买A、B两种型号的污水处理设备共20台，每台A型污水处理设备12万元，每台B型污水处理设备10万元，已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨，2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨．

(1)、求A、B两种型号污水处理设备每周分别可以处理污水多少吨？

(2)、现要求购买A种型号污水处理设备的台数不少于B种型号污水处理设备台数的2倍，问如何设计购买方案，使购买这两种型号污水处理设备的费用最少，最少费用是多少？

查看试题解析
22. 定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．

(1)、如图1，在△ABC中，AB＝AC，AD是△ABC的中线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．

(2)、如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB为邻余线，E，F在格点上．

查看试题解析
23. 综合与实践

(1)、操作发现：
已知点P为正方形ABCD的边AD或CD上的一个动点（点A，D，C除外），作射线BP，作AE⊥BP于点E，CF⊥BP于点F．

如图1，当点P在CD上（点C，D除外）运动时，直接写出线段AE，CF，EF间的数量关系．

(2)、如图2，当点P在AD上（点A，D除外）运动时，线段AE，CF，EF又有怎样的数量关系？写出结论并说明理由．

(3)、拓广探索：
如图3，若点P为矩形ABCD的边CD上（点C，D除外）一点，其它条件不变，已知AB＝6，BC＝8，BP＝ $4 \sqrt{5}$ ，求AE的长．

查看试题解析