山西省临汾市襄汾县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 已知分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±12. 科学家在实验室检测出新型冠状病毒的直径为0.000000125m , 用科学记数法表示为( )A、1.25×10﹣6m B、1.25×10﹣7m C、125×10﹣8m D、125×10﹣9m3. 如图,平行四边形ABCD的对角线AC与BD相交于点O , 添加一个条件不能使平行四边形ABCD变为矩形的是( )
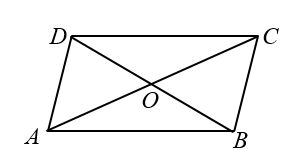 A、OA=OC B、AC=BD C、DA⊥AB D、∠OAB=∠OBA4. 某校艺术节举行歌唱比赛,八年级的10名学生参赛成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
A、OA=OC B、AC=BD C、DA⊥AB D、∠OAB=∠OBA4. 某校艺术节举行歌唱比赛,八年级的10名学生参赛成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )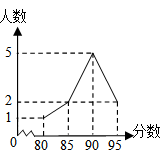 A、平均数是90 B、中位数是90 C、众数是90 D、方差是195. 如图,在平行四边形ABCD中,对角线AC的垂直平分线分别交CD、AB于点E、F , 连接CF . 若△BCF的周长为3,则平行四边形ABCD的周长为( )
A、平均数是90 B、中位数是90 C、众数是90 D、方差是195. 如图,在平行四边形ABCD中,对角线AC的垂直平分线分别交CD、AB于点E、F , 连接CF . 若△BCF的周长为3,则平行四边形ABCD的周长为( ) A、15 B、12 C、9 D、66. 化简 的结果为( )A、x﹣y B、x+y C、 D、7. 如图,直线l⊥x轴于点P , 且与反比例函数 = (x>0)及 = (x>0)的图象分别交于点A、B , 连接OA、OB , 若△OAB的面积为3,则k1﹣k2的值为( )
A、15 B、12 C、9 D、66. 化简 的结果为( )A、x﹣y B、x+y C、 D、7. 如图,直线l⊥x轴于点P , 且与反比例函数 = (x>0)及 = (x>0)的图象分别交于点A、B , 连接OA、OB , 若△OAB的面积为3,则k1﹣k2的值为( )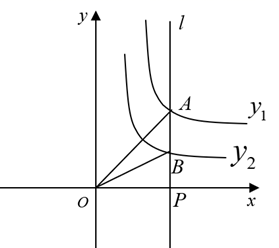 A、 B、3 C、6 D、98. 若点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(3k+2)x+k的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在平行四边形ABCD中,E为BC边上一点(不与端点重合),若AB=AE , 且AE平分∠DAB , 则下列结论:①∠B=60°,②AC=BC , ③∠AED=∠ACD , ④△ABC≌△EAD . 其中正确的个数是( )
A、 B、3 C、6 D、98. 若点M(k﹣1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(3k+2)x+k的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在平行四边形ABCD中,E为BC边上一点(不与端点重合),若AB=AE , 且AE平分∠DAB , 则下列结论:①∠B=60°,②AC=BC , ③∠AED=∠ACD , ④△ABC≌△EAD . 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个10. 如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )
A、1个 B、2个 C、3个 D、4个10. 如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是( )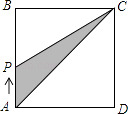 A、
A、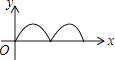 B、
B、 C、
C、 D、
D、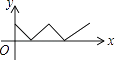
二、填空题
-
11. 为了解某班学生体育锻炼的用时情况,收集了该班学生一天用于体育锻炼的时间(单位:小时),整理成如图的统计图.则该班学生这天用于体育锻炼的平均时间为小时.
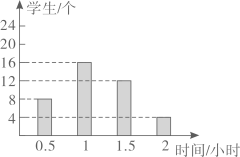 12. 某工程队修建一条长1200m的道路;采用新的施工方式,工效提升了50%,结果提前4天完成任务,设这个工程队原计划每天修建道路xm , 则列出的方程为 .13. 如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为.
12. 某工程队修建一条长1200m的道路;采用新的施工方式,工效提升了50%,结果提前4天完成任务,设这个工程队原计划每天修建道路xm , 则列出的方程为 .13. 如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为.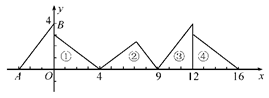 14. 已知P1(x1 , y1),P2(x2 , y2),P3(x3 , y3)是反比例函数 的图象上的三点,且x1<0<x2<x3 , 则y1 , y2 , y3的大小关系是.15. 如图,矩形ABCD中,AB=4,BC=6,E是边AD的中点,将△ABE折叠后得到△A′BE,延长BA′交CD于点F,则DF的长为 .
14. 已知P1(x1 , y1),P2(x2 , y2),P3(x3 , y3)是反比例函数 的图象上的三点,且x1<0<x2<x3 , 则y1 , y2 , y3的大小关系是.15. 如图,矩形ABCD中,AB=4,BC=6,E是边AD的中点,将△ABE折叠后得到△A′BE,延长BA′交CD于点F,则DF的长为 .
三、解答题
-
16.(1)、计算: ;(2)、解方程: ﹣1= .17. 先化简再求值 ,其中x=-3.18. 某班实行小组量化考核制.为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
综合评价得分统计表(单位:分)
周次
组别
一
二
三
四
五
六
甲组
12
15
16
14
14
13
乙组
9
14
10
17
16
18
(1)、请根据表中的数据完成下表(注:方差的计算结果精确到0.1)平均数
中位数
方差
甲组
14
乙组
14
11.7
(2)、根据综合评价得分统计表中的数据,请在如图中画出乙组综合评价得分的折线统计图. (3)、根据折线统计图中的信息,请你分别对甲、乙两个小组连续六周的学习情况作出简要评价.19. 今年新冠肺炎疫情在全球肆虐,为降低病亡率,某工厂平均每天比原计划多生产5台呼吸机,现在生产60台呼吸机的时间与原计划生产45台呼吸机所需时间相同.求该工厂原来平均每天生产多少台呼吸机?20. 如图,在▱ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(3)、根据折线统计图中的信息,请你分别对甲、乙两个小组连续六周的学习情况作出简要评价.19. 今年新冠肺炎疫情在全球肆虐,为降低病亡率,某工厂平均每天比原计划多生产5台呼吸机,现在生产60台呼吸机的时间与原计划生产45台呼吸机所需时间相同.求该工厂原来平均每天生产多少台呼吸机?20. 如图,在▱ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .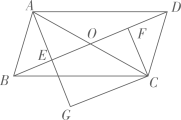 (1)、求证: △ABE≌△CDF ;(2)、当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.21. 有这样一个问题:探究函数y= 的图象与性质.小慧根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)、求证: △ABE≌△CDF ;(2)、当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.21. 有这样一个问题:探究函数y= 的图象与性质.小慧根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小慧的探究过程,请补充完成: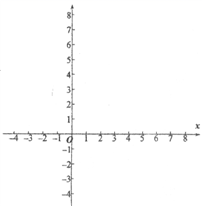 (1)、函数y= 的自变量x的取值范围是;(2)、列出y与x的几组对应值.请直接写出m的值,m=;
(1)、函数y= 的自变量x的取值范围是;(2)、列出y与x的几组对应值.请直接写出m的值,m=;x
…
-3
-2
0
1
1.5
2.5
m
4
6
7
…
y
…
2.4
2.5
3
4
6
-2
0
1
1.5
1.6
…
(3)、请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;(4)、结合函数的图象,写出该函数的两条性质:①;
② .
22. 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.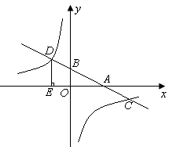 (1)、求反比例函数与一次函数的解析式.(2)、根据图象写出不等式kx+b> 的解集.(3)、连接OC、OD,求 的面积.23. 阅读下列材料:
(1)、求反比例函数与一次函数的解析式.(2)、根据图象写出不等式kx+b> 的解集.(3)、连接OC、OD,求 的面积.23. 阅读下列材料: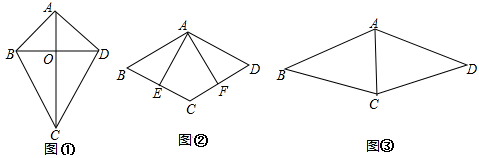
如图①,在四边形ABCD中,若AB=AD , BC=CD , 则把这样的四边形称为筝形.
(1)、写出筝形的两个性质(定义除外):①;
② .
(2)、如图②,在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF , ∠AEC=∠AFC . 求证:四边形AECF是筝形.(3)、如图③,在筝形ABCD中,AB=AD=15,BC=DC=13,AC=14,求筝形ABCD的面积.