内蒙古自治区乌海市海勃湾区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、2 B、-2 C、4 D、-42. 如图,在数轴上点A , B所表示的数分别为-1,1,CB⊥AB , BC=1,以点A为圆心,AC长为半径画弧,交数轴于点D(点D在点B的右侧),则点D所表示的数是( )
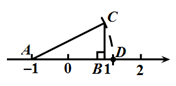 A、 B、 C、 D、3. 若a+|a|=0,则化简 的结果为( )A、1 B、−1 C、1−2a D、2a−14. 点点同学对数据25,43,28,2□,43,36,52进行统计分析,发现其中一个两位数的个位数被墨水涂污看不到了,则计算结果与涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数5. 下列命题①若a>b,则ac>bc;②若a=1,则 =a;③ 的平方根是 ④各边都相等的多边形是正多边形,其中真命题的个数是( )A、0 B、1 C、2 D、36. 某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩 及其方差 如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
A、 B、 C、 D、3. 若a+|a|=0,则化简 的结果为( )A、1 B、−1 C、1−2a D、2a−14. 点点同学对数据25,43,28,2□,43,36,52进行统计分析,发现其中一个两位数的个位数被墨水涂污看不到了,则计算结果与涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数5. 下列命题①若a>b,则ac>bc;②若a=1,则 =a;③ 的平方根是 ④各边都相等的多边形是正多边形,其中真命题的个数是( )A、0 B、1 C、2 D、36. 某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩 及其方差 如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )甲
乙
丙
丁
8
9
9
8
1
1
1.2
1.3
A、甲 B、乙 C、丙 D、丁7.如图,四边形ABCD中,∠DAB=60°,∠B=∠D=90°, BC=1, CD=2,则对角线AC的长为( )
 A、 B、 C、 D、8. 平面直角坐标系中,过点(-2,3)的直线
A、 B、 C、 D、8. 平面直角坐标系中,过点(-2,3)的直线 经过一、二、三象限,若点(0,a),(-1,b),(c,-1)都在直线
经过一、二、三象限,若点(0,a),(-1,b),(c,-1)都在直线  上,则下列判断正确的是( ) A、a<b B、a<3 C、b<3 D、c<-29. 若代数式 在实数范围内有意义,则一次函数 的图象可能是( )A、
上,则下列判断正确的是( ) A、a<b B、a<3 C、b<3 D、c<-29. 若代数式 在实数范围内有意义,则一次函数 的图象可能是( )A、 B、
B、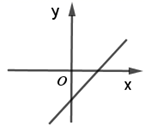 C、
C、 D、
D、 10. 如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F , 连结CE , DF , 下列说法错误的是( )
10. 如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F , 连结CE , DF , 下列说法错误的是( )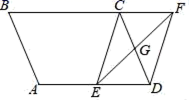 A、四边形CEDF是平行四边形 B、当CE⊥AD时,四边形CEDF是矩形 C、当∠AEC=120°时,四边形CEDF是菱形 D、当AE=ED时,四边形CEDF是菱形11. 在同一直角坐标系内,若直线y=2x-1与直线y=-2x+m的交点在第四象限,则m的取值范围是( )A、m>—1 B、m<1 C、—1<m<1 D、—1≤m≤112. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )
A、四边形CEDF是平行四边形 B、当CE⊥AD时,四边形CEDF是矩形 C、当∠AEC=120°时,四边形CEDF是菱形 D、当AE=ED时,四边形CEDF是菱形11. 在同一直角坐标系内,若直线y=2x-1与直线y=-2x+m的交点在第四象限,则m的取值范围是( )A、m>—1 B、m<1 C、—1<m<1 D、—1≤m≤112. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )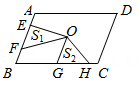 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 某班有50名学生,平均身高为166cm,其中20名女生的平均身高为160cm,则30名男生的平均身高为cm.14. 已知一直角三角形的两边分别为3和4,则第三边长的平方是;15. 已知P(a , b)是直线 上的点,则4b-2a+3的值为 .16. 若x,y为实数,且y= ,则x-y= .17. 已知函数 与函数 的图象交于点P,则不等式 的解集是 .
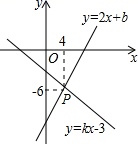 18. 若一次函数y=kx+b,当-3≤x≤1时,对应的y值满足1≤y≤9,则一次函数的解析式为.19. 在菱形 中, ,点 是 的中点, 是对角线 上的一个动点,则 的最小值为 .
18. 若一次函数y=kx+b,当-3≤x≤1时,对应的y值满足1≤y≤9,则一次函数的解析式为.19. 在菱形 中, ,点 是 的中点, 是对角线 上的一个动点,则 的最小值为 .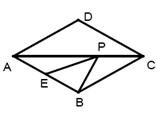 20. 在锐角三角形ABC中,AH是边BC的高,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC.其中正确的是 .
20. 在锐角三角形ABC中,AH是边BC的高,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC.其中正确的是 .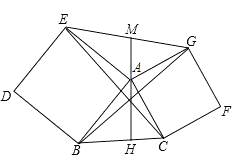
三、解答题
-
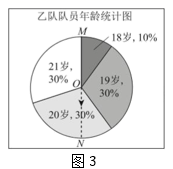
21. 计算题:(1)、(2)、22. 甲、乙两支运动队各有10名队员,他们的年龄分布情况分别如图、表所示:
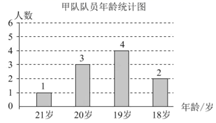
甲、乙两队队员年龄统计表
平均数(近似值)
众数
中位数
甲队
a
①
②
乙队
20
③
b
解决下列问题:
(1)、求甲队队员的平均年龄a的值.(结果取整数)(2)、补全统计表中的①②③三处.(3)、阅读理解-----扇形图中求中位数的方法.[阅读与思考]
小明同学在求乙队队员年龄的中位数b时,是这样思考的:因为中位数是将一组数据按大小排序后,排在中间位置的一个数或中间两个数的平均数,那就需要先找到数据按大小排序后,大致排在50%附近的数,再根据中位数的概念进行细化求解.
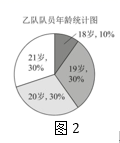
图2这个扇形图中的数据18~21是按大小顺序旋转排列的,我们就可以像图3所示的这样,先找到最大数据“21”与最小数据“18”的分界半径OM,为找到排在50%附近的数,再作出直径MN,那么射线ON指向的数据就是中位数.
王老师的评价:小明的这个方法是从中位数的概念出发,充分利用了扇形图的特性形象直观地解决问题.
[理解与应用]
请你利用小明的方法直接写出统计表中b的值.
 23. 若△ABC三边长为a,b,c满足a2+b2+c2+200=12a+16b+20c,试判断△ABC的形状.24. 抗击“新冠疫情”期间,某种消毒液A市需要6吨,B市需要8吨,正好M市储备有10吨,N市储备有4吨,预防“新冠疫情”领导小组决定将这14吨消毒液调往A市和B市,消毒液每吨的运费价格如下表。设从M市调运x吨到A市.
23. 若△ABC三边长为a,b,c满足a2+b2+c2+200=12a+16b+20c,试判断△ABC的形状.24. 抗击“新冠疫情”期间,某种消毒液A市需要6吨,B市需要8吨,正好M市储备有10吨,N市储备有4吨,预防“新冠疫情”领导小组决定将这14吨消毒液调往A市和B市,消毒液每吨的运费价格如下表。设从M市调运x吨到A市.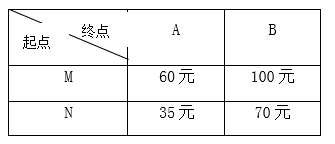 (1)、求调运14吨消毒液的总运费y关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费的多少?25. 正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到
(1)、求调运14吨消毒液的总运费y关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费的多少?25. 正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到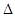 BFD.
(1)、在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表:
BFD.
(1)、在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表: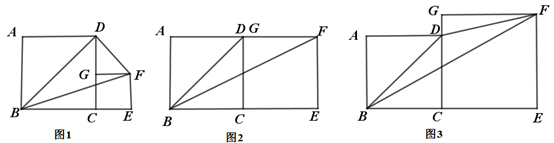
正方形CEFG的边长
1
3
4
 BFD的面积(2)、若正方形CEFG的边长为a,正方形ABCD的边长为 ,猜想 的大小,并结合图3证明你的猜想.26. 如图,直线y=﹣2x+8分别交x轴,y轴于点A , B , 直线y x+3交y轴于点C , 两直线相交于点D .
BFD的面积(2)、若正方形CEFG的边长为a,正方形ABCD的边长为 ,猜想 的大小,并结合图3证明你的猜想.26. 如图,直线y=﹣2x+8分别交x轴,y轴于点A , B , 直线y x+3交y轴于点C , 两直线相交于点D .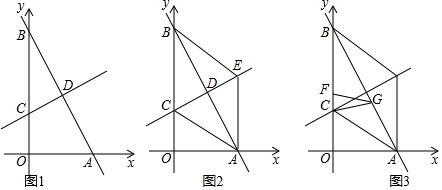 (1)、求点D的坐标;(2)、如图2,过点A作AE∥y轴交直线y x+3于点E , 连接AC , BE . 求证:四边形ACBE是菱形;(3)、如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG , FG , 当CG=FG , 且∠CGF=∠ABC时,求点G的坐标.
(1)、求点D的坐标;(2)、如图2,过点A作AE∥y轴交直线y x+3于点E , 连接AC , BE . 求证:四边形ACBE是菱形;(3)、如图3,在(2)的条件下,点F在线段BC上,点G在线段AB上,连接CG , FG , 当CG=FG , 且∠CGF=∠ABC时,求点G的坐标.