内蒙古霍林郭勒市初中联盟校2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 使代数式 有意义的x的取值范围( )A、x>2 B、x≥2 C、x>3 D、x≥2且x≠32. 下列计算正确的是( )A、 B、 C、 D、3. 满足下列条件的 ,不是直角三角形的是( )A、 B、 C、 D、4. 关于一次函数 ,下列说法正确的是( )A、它的图象过点 B、它的图象经过第一、二、三象限 C、 随 的增大而增大 D、当 时,总有5. 下列说法正确的是( )A、了解某班学生的身高情况,适宜采用抽样调查 B、数据3,5,4,1,1的中位数是4 C、数据5,3,5,4,1,1的众数是1和5 D、甲、乙两人射中环数的方差分别为s甲2=2,s乙2=3,说明乙的射击成绩比甲稳定6. 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
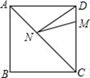 A、6 B、8 C、12 D、107. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中 表示时间, 表示林茂离家的距离。依据图中的信息,下列说法错误的是( )
A、6 B、8 C、12 D、107. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中 表示时间, 表示林茂离家的距离。依据图中的信息,下列说法错误的是( )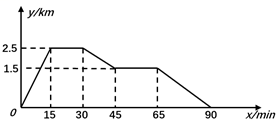 A、体育场离林茂家2.5km B、体育场离文具店1km C、林茂从体育场出发到文具店的平均速度是50m/min D、林茂从文具店回家的平均速度是60m/min8. 已知一次函数 的图象如图所示,则一次函数 的图象大致是( )
A、体育场离林茂家2.5km B、体育场离文具店1km C、林茂从体育场出发到文具店的平均速度是50m/min D、林茂从文具店回家的平均速度是60m/min8. 已知一次函数 的图象如图所示,则一次函数 的图象大致是( )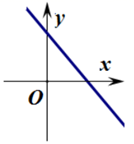 A、
A、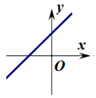 B、
B、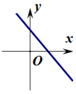 C、
C、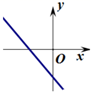 D、
D、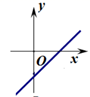 9. 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
9. 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )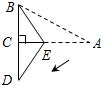 A、6 B、3 C、 D、10. 如图所示,矩形ABCD中,AE平分 交BC于E, ,则下面的结论:① 是等边三角形;② ;③ ;④ ,其中正确结论有( )
A、6 B、3 C、 D、10. 如图所示,矩形ABCD中,AE平分 交BC于E, ,则下面的结论:① 是等边三角形;② ;③ ;④ ,其中正确结论有( )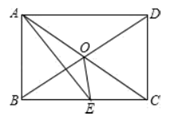 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
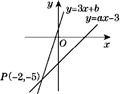
11. 计算:=12. 直角三角形的两边长分别为3和5,则第三条边长是.13. 点A(-3,a)和点B(2,b)均在一次函数 的图象上,则ab . (填“>”,“<”或“=”)14. 已知菱形 的边长为4,∠A=60°,则菱形 的面积为 .15. 已知一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的中位数是 .16. 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是 .
 17. 在数轴上表示实数a的点如图所示,化简 +|a-2|的结果为 .
17. 在数轴上表示实数a的点如图所示,化简 +|a-2|的结果为 . 18. 如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=s时,△PBQ为直角三角形.
18. 如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=s时,△PBQ为直角三角形.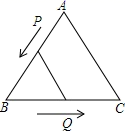
三、解答题
-
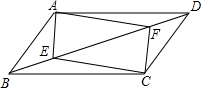
19. 计算下列各式(1)、(2)、20. 如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
 21. 为了解中学生“平均每天体育锻炼时间”的情况,某地区教育部门随机调查了若干名中学生,根据调查结果制作统计图①和图②,请根据相关信息,解答下列问题:
21. 为了解中学生“平均每天体育锻炼时间”的情况,某地区教育部门随机调查了若干名中学生,根据调查结果制作统计图①和图②,请根据相关信息,解答下列问题: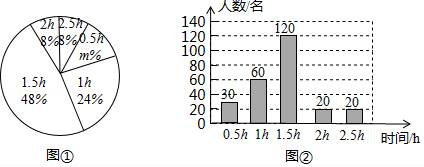 (1)、本次接受随机抽样调查的中学生人数为 , 图①中m的值是;(2)、求本次调查获取的样本数据的平均数、众数和中位数;(3)、根据统计数据,估计该地区250000名中学生中,每天在校体育锻炼时间大于等于1.5h的人数.22. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、本次接受随机抽样调查的中学生人数为 , 图①中m的值是;(2)、求本次调查获取的样本数据的平均数、众数和中位数;(3)、根据统计数据,估计该地区250000名中学生中,每天在校体育锻炼时间大于等于1.5h的人数.22. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.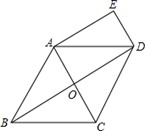 (1)、求证:四边形AODE是矩形;(2)、若AB=12,∠BCD=120°,求四边形AODE的面积23. 如图,直线 的解析表达式为 ,且 与 轴交于点 ,直线 经过点 ,直线 , 交于点 .
(1)、求证:四边形AODE是矩形;(2)、若AB=12,∠BCD=120°,求四边形AODE的面积23. 如图,直线 的解析表达式为 ,且 与 轴交于点 ,直线 经过点 ,直线 , 交于点 .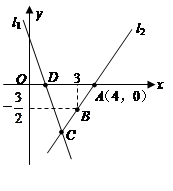 (1)、求点 的坐标;(2)、求直线 的解析表达式;(3)、求 的面积.24. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、求点 的坐标;(2)、求直线 的解析表达式;(3)、求 的面积.24. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、该网店甲、乙两种羽毛球每筒的售价各是多少元?(2)、根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
25. 如图,在梯形ABCD中,AD∥BC , AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.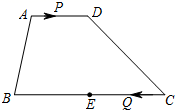 (1)、当运动时间t为多少秒时,PQ∥CD .(2)、当运动时间t为多少秒时,以点P , Q , E , D为顶点的四边形是平行四边形.
(1)、当运动时间t为多少秒时,PQ∥CD .(2)、当运动时间t为多少秒时,以点P , Q , E , D为顶点的四边形是平行四边形.