浙江省湖州市长兴县2021届九年级上学期数学开学试卷
试卷更新日期：2020-09-14 类型：开学考试
一、选择题(每小题3分，共30分)
-
1. 若二次根式 有意义，则实数x的取值范围是（ ）A、x≠8 B、x≥8 C、x≤8 D、x=82. 甲、乙、丙、丁四名学生近5次数学成绩的平均数都是110分，方差如表，则这四名学生成绩最稳定的是（ ）
学生
甲
乙
丙
丁
方差(s2)
11.6
6.8
7.6
2.8
A、甲 B、乙 C、丙 D、丁3. 将抛物线y=2(x-3)2+2向左平移3个单位长度，再向下平移2个单位长度，得到拋物线的解析式是（ ）A、y=2(x-6)2 B、y=2(x-6)2+4 C、y= 2x2 D、y=2x2+44. 已知关于x的一元二次方程x2+bx-1=0，则下列关于该方程根的判断，正确的是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关5. 若正比例函数y=kx经过点(-2，1)，则它与反比例函数y= 的图象的两个交点分别在（ ）A、第一、二象限 B、第二、四象限 C、第一、三象限 D、第三、四象限6. 平行四边形、矩形、菱形、正方形共有的性质是（ ）A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线互相垂直平分7. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC'D'，若∠D'AB=30°，则菱形ABC'D'的面积与正方形ABCD的面积之比是（ ）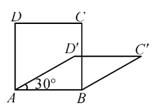
A、1 B、 C、 D、8. 若点A(-2，y1)，B(1，y2)，C(2，1)在反比例函数y= 的图象上，则（ ）A、y2<y1<1 B、y1<y2<1 C、1<y2<y1 D、y1<1<y29. 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”，已知正方形ABCD的边长为4，则图2中h的值为（ ）
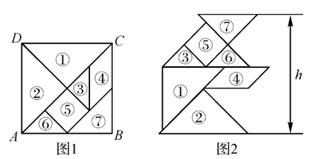A、6 B、4 C、4+ D、810. 如图，正方形四个顶点的坐标依次为(1，1)，(3，1)，(3，3)，(1，3)，若抛物线y=ax2的图象与正方形有公共点，则实数a的取值范围是（ ）
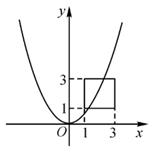A、 ≤a≤3 B、 ≤a≤1 C、 ≤a≤3 D、 ≤a≤1二、填空题(每小题4分，共24分)
-
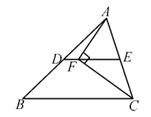
11. 已知一组数据的方差是4，则这组数据的标准差是。12. 抛物线y=3(x-1)2+8的顶点坐标为 。13. 一个五边形所有内角都相等，它的每一个内角等于。14. 某商店4月份营业额为2.7万元，6月份营业额为3.5万元，平均每月的增长率为 ，根据题意可列方程为.15. 如图，DE为△ABC的中位线，点F在DE上，且∠AFC为直角，若DF=2cm，BC=16cm，则AC的长为cm。
16. 如图，已知在平面直角坐标系xOy中，Rt△OAB的直角顶点B在x轴的正半轴上，点A在第一象限，反比例函数y= (x>0)的图象经过OA的中点C，交AB于点D，连结CD，若△ACD的面积是2，则k的值是。
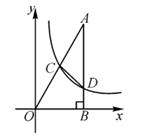
三、解答题(共66分)
-
17. 计算:(1)、(2)、(2- )(3+2 )18. 解方程:(1)、2x2-5x+3=0；(2)、(x+1)2=4x19. 为了了解某校八年级学生每周平均课外阅读时间的情况，随机抽取了50名八年级学生，对其每周平均课外阅读时间进行统计，并绘制成下面的统计图。
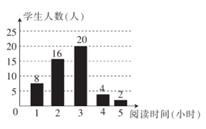(1)、这50名同学每周阅读时间的众数为小时，中位数为小时。(2)、求出这组数据的平均数。20. 如图，在5×5的网格中，△ABC的三个顶点都在格点上。
(1)、在图1中画出一个以AB为边的 ABDE，使顶点D，E在格点上。(2)、在图2中画出一条恰好平分△ABC周长的直线l(至少经过两个格点)。21. 如图，已知反比例函数y= 的图象与直线y=ax+b相交于点A(-2，3)，B(1，m)。
(1)、求出直线y=ax+b的表达式；(2)、在x轴上有一点P使得△PAB的面积为18，求出点P的坐标。22. 某商店销售一款口罩，每袋的进价为12元.经市场调查发现，每袋售价每增加1元，日均销售量减少5袋.当售价为每袋18元时，日均销售量为100袋.设口罩每袋的售价为x元，日均销售量为y袋.(1)、用含x的代数式表示y；(2)、物价部门规定，该款口罩的每袋售价不得高于22元.当每袋售价定为多少元时，商店销售该款口罩所得的日均毛利润为720元？23. 已知：如图，抛物线y=ax2+4x+c经过原点O(0，0)和点A (3，3)，P为拋物线上的一个动点，过点P作x轴的垂线，垂足为B(m，0)，并与直线OA交于点C。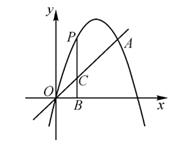
(1)、求抛物线的解析式；(2)、当点P在直线OA上方时，求线段PC的最大值。24. 在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合(如图1)，其中∠ACB=∠DFE=90° ，BC=EF=3cm，AC=DF=4 cm，并进行如下研究活动。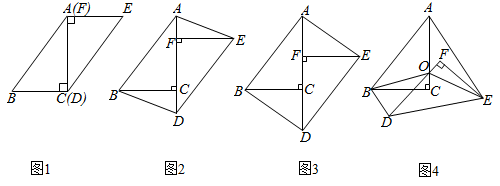
活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD(如图2)，当点F与点C重合时停止平移。
活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转a度(0≤a≤90)，连结OB，OE(如图4)。
(1)、图2中的四边形ABDE是平行四边形吗？请说明理由。(2)、当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形(如图3)。求AF的长。(3)、当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由。