黑龙江省哈尔滨市香坊区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、x+2y＝1 B、x²+2＝0 C、x²+ $\frac{1}{x}$ ＝2 D、3x+8＝2x+2

查看试题解析
2. 若正比例函数y=kx的图象经过点（1，2），则k的值为（）

A、 $- \frac{1}{2}$ B、－2 C、 $\frac{1}{2}$ D、2

查看试题解析
3. 下列四组线段中，可以构成直角三角形的是（）

A、1，4，9 B、1， $\sqrt{2}$ ，2 C、1， $\sqrt{3}$ ，2 D、5，11，12

查看试题解析
4. 下列各组条件中，不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B ∥ C D$ ， $A D ∥ B C$ B、 $A B ∥ C D$ ， $A D = B C$ C、 $A B ∥ C D$ ， $A B = C D$ D、 $A B = C D$ ， $A D = B C$

查看试题解析
5. 一元二次方程 $x^{2} + x - 4 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
6. 一个矩形的长比宽多2cm ，面积是7cm² ．若设矩形的宽为xcm ，则可列方程（）

A、x（x+2）＝7 B、x（x﹣2）＝7 C、 $\frac{1}{2}$ x（x+2）＝7 D、 $\frac{1}{2}$ x（x﹣2）＝7

查看试题解析
7. 在平面直角坐标系中，一次函数y=kx+b的图象如图所示，则k和b的取值范围是（）

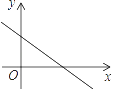A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
8. 下列命题中，真命题的是（）

A、四条边相等的四边形是正方形 B、对角线相等的四边形是矩形 C、一条对角线平分一组对角的四边形是菱形 D、一组对边平行，一组对角相等的四边形是平行四边形

查看试题解析
9. 菱形的周长为8厘米，两相邻角度数比是1：2，则菱形的面积是（）平方厘米．

A、2 $\sqrt{3}$ B、2 $\sqrt{2}$ C、4 $\sqrt{2}$ D、4 $\sqrt{3}$

查看试题解析
10. 周日，小涛从家沿着一条笔直的公路步行去报亭看报，看了一段时间后，他按原路返回家中，小涛离家的距离y（单位：m）与他所用的时间t（单位：min）之间的函数关系如图所示，下列说法中正确的是（）

A、小涛家离报亭的距离是900m B、小涛从家去报亭的平均速度是60m/min C、小涛从报亭返回家中的平均速度是80m/min D、小涛在报亭看报用了15min

查看试题解析

二、填空题

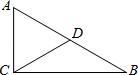
11. 函数y= $\frac{1}{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 将矩形添加一个适当的条件：，能使其成为正方形．

查看试题解析
13. 一次函数y＝2x+4与x轴的交点坐标是．

查看试题解析
14. 已知方程ax²+bx+c＝0的一个根是﹣1，则a﹣b+c＝．

查看试题解析
15. 在直角三角形ABC中，斜边AB=1，则AB²+BC²+AC²的值是．

查看试题解析
16. 如图，在△ABC中，∠ACB＝90°，∠B＝40°，D为线段AB的中点，则∠ACD＝．

查看试题解析
17. 某乡村种的水稻2018年平均每公顷产3200kg ， 2020年平均每公顷产5000kg ，则水稻每公顷产量的年平均增长率为．

查看试题解析
18. 一个三角形的两边的长分别是3和5，要使这个三角形为直角三角形，则第三条边的长为．

查看试题解析
19. 如图，一次函数y＝﹣2x和y＝kx+b的图象相交于点A（m ， 3），则关于x的方程kx+b+2x＝0的解为．

查看试题解析
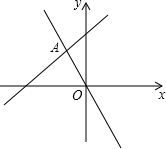20. 如图，将矩形ABCD沿AE折叠，使点D落在BC边的点F处，过F作FG∥CD交AE于点G ，连接DG ．若AG＝3 $\sqrt{5}$ ，FG＝5，则AE的长为．

查看试题解析

三、解答题

21. 用适当的方法解方程：

(1)、x²﹣4x﹣7＝0；

(2)、3x（2x+1）＝4x+2．

查看试题解析
22. 如图，将一个2×2的正方形剪成四个全等的直角三角形，请用这四个全等的直角三角形，在图①、图②的网格中，拼出两个不全等且含有正方形的图形．要求拼图时，直角三角形的顶点均在小正方形的顶点上，且四个直角三角形不能有重叠部分．

查看试题解析
23. 我们知道，以3，4，5为边长的三角形是直角三角形，称3，4，5为勾股数组，记为（3，4，5），可以看作（2²﹣1，2×2，2²+1）；同时8，6，10也为勾股数组，记为（8，6，10），可以看作（3²﹣1，2×3，3²+1）．类似的，依次可以得到第三个勾股数组（15，8，17）．

(1)、请你根据上述勾股数组规律，写出第5个勾股数组；

(2)、若设勾股数组中间的数为2n（n≥2，且n为整数），根据上述规律，请直接写出这组勾股数组．

查看试题解析
24. 如图，AD是△ABC的中线，AE∥BC ， BE交AD于点F ， F是AD的中点，连接EC ．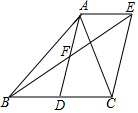

(1)、求证：四边形ADCE是平行四边形；

(2)、若四边形ABCE的面积为S ，请直接写出图中所有面积是 $\frac{1}{3}$ S的三角形．

查看试题解析
25. 某商店销售一台A型电脑销售利润为100元，销售一台B型电脑的销售利润为150元．该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的3倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．

(1)、求y关于x的函数关系式；

(2)、该商店购进A型、B型电脑各多少台，才能使销售总利润最大？

查看试题解析
26. 在正方形ABCD中，连接AC ，点E在线段AD上，连接BE交AC于M ，过点M作FM⊥BE交CD于F ．

(1)、如图①，求证：∠ABE+∠CMF＝∠ACD；

(2)、如图②，求证：BM＝MF；

(3)、如图③，连接BF ，若点E为AD的中点，AB＝6，求BF的长．

查看试题解析
27. 如图①，在平面直角坐标系中，点A在直线y＝﹣ $\frac{4}{3}$ x上，且点A的横坐标为﹣6，直线AB分别交x轴、y轴于点B和点C ．点B的坐标为（10，0）．

(1)、求直线AB的解析式；

(2)、如图②，点D坐标为（4，8），连接AD、BD ，动点P从点A出发，沿线段AD运动．过点P作x轴的垂线，交AB于点Q ，连接DQ ．设△BDQ的面积为S（S≠0），点P的横坐标为t ，求S与t之间的函数关系式；

(3)、在（2）的条件下，连接PC ，若∠CPD+∠OBD＝90°，求t的值．

查看试题解析