黑龙江省哈尔滨市阿城区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 一个直角三角形的两条直角边分别是5和12,则斜边是( )A、13 B、12 C、15 D、102. 下列四个图象中,不表示某一函数图象的是( )
A、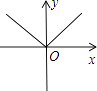 B、
B、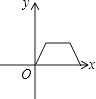 C、
C、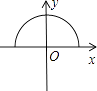 D、
D、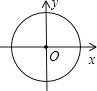 3. 下列方程中是关于x的一元二次方程的是( )A、 B、ax2+bx+c=0 C、(x-1)(x+ 2)=1 D、3x2-2xy-5y2=04. 一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
3. 下列方程中是关于x的一元二次方程的是( )A、 B、ax2+bx+c=0 C、(x-1)(x+ 2)=1 D、3x2-2xy-5y2=04. 一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( ) A、x<0 B、x>0 C、x<2 D、x>25. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、每条对角线平分一组对角 D、对角线相等6. 已知,点(﹣2,y1)和点(﹣3,y2)在直线y=﹣3x+4图象上,则y1和y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定7. 如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )
A、x<0 B、x>0 C、x<2 D、x>25. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、每条对角线平分一组对角 D、对角线相等6. 已知,点(﹣2,y1)和点(﹣3,y2)在直线y=﹣3x+4图象上,则y1和y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定7. 如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )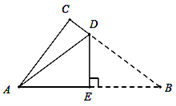 A、4㎝ B、5㎝ C、6㎝ D、 ㎝8. 某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
A、4㎝ B、5㎝ C、6㎝ D、 ㎝8. 某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
A、200(1+x)2=1000 B、200+200×2x=1000 C、200+200×3x=1000 D、200[1+(1+x)+(1+x)2]=10009. 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN , 则折痕MN的长是( ) A、5 cm B、5 cm C、4 cm D、4 cm10. 某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程(千米)与时间(分)的关系的图象,根据图象信息,下列说法正确的是( )
A、5 cm B、5 cm C、4 cm D、4 cm10. 某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程(千米)与时间(分)的关系的图象,根据图象信息,下列说法正确的是( ) A、小王去时的速度大于回家的速度 B、小王在朋友家停留了10分钟 C、小王去时所花时间少于回家所花时间 D、小王去时走上坡路施,回家时走下坡路
A、小王去时的速度大于回家的速度 B、小王在朋友家停留了10分钟 C、小王去时所花时间少于回家所花时间 D、小王去时走上坡路施,回家时走下坡路二、填空题
-
11. 在函数 中,自变量x的取值范围是.12. 已知关于x的方程x2+mx-6=0的一个根为2,则m= .13. 如图,在平行四边形ABCD中,BC=10,AC=8,BD=14,△AOD的周长是.
 14. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是 .15. 如图,等边△DEC在正方形ABCD内,连接EA、EB , 则∠AEB的度数是 .
14. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是 .15. 如图,等边△DEC在正方形ABCD内,连接EA、EB , 则∠AEB的度数是 . 16. 直线y=2x+b与x轴交于点A , 与y轴正半轴交于点B , 若△AOB的面积是12,则b= .17. 有一人患流感,经过两轮传染后共有81人患了流感,则每轮传染中平均一人传染了人.18. 已知△ABC中AB=4 ,AC=5,BC上的高为4,则BC= .19. 等边三角形ABC外一点D , ∠ADC=90°,BE⊥CD于E , AD=1,DE=2 ,则BE= .
16. 直线y=2x+b与x轴交于点A , 与y轴正半轴交于点B , 若△AOB的面积是12,则b= .17. 有一人患流感,经过两轮传染后共有81人患了流感,则每轮传染中平均一人传染了人.18. 已知△ABC中AB=4 ,AC=5,BC上的高为4,则BC= .19. 等边三角形ABC外一点D , ∠ADC=90°,BE⊥CD于E , AD=1,DE=2 ,则BE= .
三、解答题
-
20. 如图,在△ABC中,D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G , CF=2,则BC= .
 21. 解方程:(1)、x2﹣2x﹣4=0;(2)、2x2﹣7x﹣4=0.22. 图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上,请在图1、图2中各取一点C(点C必须在小正方形的顶点上),使以A、B、C为顶点的三角形分别满足以下要求:
21. 解方程:(1)、x2﹣2x﹣4=0;(2)、2x2﹣7x﹣4=0.22. 图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上,请在图1、图2中各取一点C(点C必须在小正方形的顶点上),使以A、B、C为顶点的三角形分别满足以下要求: (1)、在图1中画一个△ABC , 使△ABC为面积为5的直角三角形;(2)、在图2中画一个△ABC , 使△ABC为钝角等腰三角形.23. 如图,菱形ABCD中,点E、F分别是BC、CD边的中点.求证:AE=AF .
(1)、在图1中画一个△ABC , 使△ABC为面积为5的直角三角形;(2)、在图2中画一个△ABC , 使△ABC为钝角等腰三角形.23. 如图,菱形ABCD中,点E、F分别是BC、CD边的中点.求证:AE=AF . 24. 已知y+5与3x+4成正比例,当x=1时,y=2.求:(1)、y与x之间的函数表达式;(2)、当x=-1时,求y的值.25. 周末,小亮一家在东昌湖游玩,妈妈在湖心岛P处观看小亮与爸爸在湖中划船(如图)小船从P处出发,沿北偏东60°方向滑行150米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏东30°的方向上.
24. 已知y+5与3x+4成正比例,当x=1时,y=2.求:(1)、y与x之间的函数表达式;(2)、当x=-1时,求y的值.25. 周末,小亮一家在东昌湖游玩,妈妈在湖心岛P处观看小亮与爸爸在湖中划船(如图)小船从P处出发,沿北偏东60°方向滑行150米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏东30°的方向上. (1)、求点P与AB距离多少米?(2)、如果小亮从A到B的速度是3米/秒,那么小亮从A到B所用的时间是多少秒?26. 商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库存,商场
(1)、求点P与AB距离多少米?(2)、如果小亮从A到B的速度是3米/秒,那么小亮从A到B所用的时间是多少秒?26. 商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元. 据此规律,请回答:
(1)、商场日销售量增加件,每件商品盈利元(用含x的代数式表示);(2)、在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?27. 如图,在平面直角坐标系中,点O为坐标原点,直线1分别交x轴、y轴于A . B两点,OA<OB , 且OA、OB的长分别是一元二次方程x2﹣14x+48=0的两根. (1)、求直线AB的解析式;(2)、点C从点A出发沿射线AB方向运动,运动的速度为每秒2个单位,设△OBC的面积S , 点C运动的时间为t , 写出S与t的函数关系式,并直接写出自变量的取值范围;(3)、点P是y轴上的点,点Q是第一象限内的点,若以A、B、P、Q为顶点的四边形是菱形请求出点Q的坐标.
(1)、求直线AB的解析式;(2)、点C从点A出发沿射线AB方向运动,运动的速度为每秒2个单位,设△OBC的面积S , 点C运动的时间为t , 写出S与t的函数关系式,并直接写出自变量的取值范围;(3)、点P是y轴上的点,点Q是第一象限内的点,若以A、B、P、Q为顶点的四边形是菱形请求出点Q的坐标.