河北省唐山市迁西县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 根据下列表述，能确定具体位置的是（）

A、实验中学东 B、南偏西30° C、东经120° D、会议室第7排，第5座

查看试题解析
2. 圆周长公式C=2πR中，下列说法正确的是（　　）

A、π、R是变量，2为常量 B、C、R为变量，2、π为常量 C、R为变量，2、π、C为常量 D、C为变量，2、π、R为常量

查看试题解析
3. 如图，在四边形 $A B C D$ 中， $A B / / C D$ ，要使四边形 $A B C D$ 是平行四边形，下列可添加的条件错误的是（）

A、 $A B ＝ C D$ B、 $A D / / B C$ C、 $∠ A ＝ ∠ C$ D、 $A D ＝ B C$

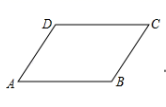查看试题解析
4. 在平面直角坐标系中，下列各点在第二象限的是（）

A、（3，1） B、（3，-1） C、（-3，1） D、（-3，-1）

查看试题解析
5. 有下列调查：其中不适合普查而适合抽样调查的是（）
①了解地里西瓜的成熟程度；②了解某班学生完成 20 道素质测评选择题的通过率；③了解一批导弹的杀伤范围；④了解迁西县中学生睡眠情况．

A、①②③ B、①②④ C、①③④ D、.②③④

查看试题解析
6. 函数 $y = \sqrt{2 x - 3}$ 中自变量 $x$ 的取值范围是（）

A、 $x \geq \frac{3}{2}$ B、 $x \geq - \frac{3}{2}$ C、 $x \leq - \frac{3}{2}$ D、 $x \leq \frac{3}{2}$

查看试题解析
7. 如图，在▱ABCD中，下列结论一定成立的是（）

A、AC⊥BD B、∠BAD+∠ABC＝180° C、AB＝AD D、∠ABC＝∠BCD

查看试题解析
8. 为了了解某校3000名学生的体重情况，从中抽取了200名学生的体重，就这个问题来说，下列说法正确的是（）

A、3000名学生是总体 B、3000名学生的体重是总体 C、每个学生是个体 D、200名学生是所抽取的一个样本

查看试题解析
9. 下列判断正确的是（）

A、对角线互相垂直的平行四边形是菱形 B、两组邻边相等的四边形是平行四边形 C、对角线相等的四边形是矩形 D、有一个角是直角的平行四边形是正方形

查看试题解析
10. 关于一次函数 $y = - 3 x + 1$ ，下列说法正确的是（）

A、图象过点 $(- 1 ， 3)$ B、 $y$ 随 $x$ 的增大而增大 C、图象经过第一、二、三象限 D、与 $y$ 轴的交点坐标为 $(0 ， 1)$

查看试题解析
11. 如图，菱形 ABCD 的顶点 C 在直线 MN 上，若∠1＝50°，∠2＝20°，则∠BDC 的度数为（）

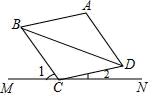A、20° B、30° C、35° D、40°

查看试题解析
12. 在平面直角坐标系中，点 A'（2，﹣2）可以由点 A（﹣2，3）通过两次平移得到，则正确的是（）

A、先向左平移4个单位长度，再向上平移5个单位长度； B、先向右平移4个单位长度，再向上平移5个单位长度； C、先向左平移4个单位长度，再向下平移 5 个单位长度； D、先向右平移4个单位长度，再向下平移 5 个单位长度．

查看试题解析
13. 下列情境分别可以用图中哪幅图来近似地刻画？①一杯越晾越凉的水（水温与时间的关系）；②一面冉冉上升的旗子（高度与时间的关系）；③足球守门员大脚开出去的球（高度与时间的关系）；④匀速行驶的汽车（速度与时间的关系），对应正确的是（）

A、 $③ ④ ① ②$ B、 $② ③ ① ④$ C、 $③ ① ④ ②$ D、 $① ② ③ ④$

查看试题解析
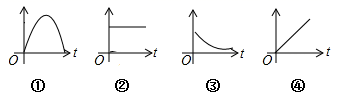14. 一次函数 $y_{1} = k x + b$ 与 $y_{2} = x + a$ 的图象如图所示，有下列结论：① $a > 0$ ；② $k > 0$ ；③当 $x < 4$ 时， $k x + b > x + a$ 其中正确的结论有（）

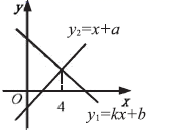A、0个 B、1个 C、2个 D、3个

查看试题解析
15. 如图，四边形 OABC 是矩形，A（2，1），B（0，5），点 C 在第二象限，则点 C 的坐标是（）

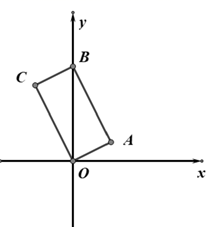A、（1，3） B、（﹣1，2） C、（﹣2，﹣3） D、（﹣2，4）

查看试题解析
16. 某校八年级同学到距学校8千米的某地参加社会实践活动，一部分同学步行，另一部分同学骑自行车，沿相同路线前往.如图， $a$ ， $b$ 分别表示步行和骑车的同学前往目的地所走的路程 $y$ （千米）与所用时间 $x$ （分钟）之间的函数图象.则下列判断错误的是（）

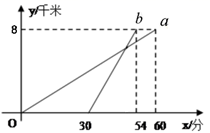A、骑车的同学比步行的同学晚出发30分钟 B、骑车的同学和步行的同学同时到达目的地 C、步行的速度是7.5千米/小时 D、骑车的同学从出发到追上步行的同学用了18分钟

查看试题解析

二、填空题

17. 点M(﹣3，﹣2)到y轴的距离是．

查看试题解析
18. 若正比例函数y=kx的图象经过点（2，4），则该函数的解析式是．

查看试题解析
19. 如图，∠1+∠2+∠3+∠4+∠5＝．

查看试题解析
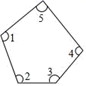20. 如图，在直线 l 上有三个正方形 m、q、n，若 m、q 的面积分别为 4 和 9，则 n的面积．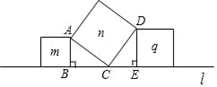

查看试题解析

三、解答题

21. 如图，在直角坐标平面内，已知点 $A$ 的坐标是 $(0 ， 3)$ ，点 $B$ 的坐标是 $(- 3 ， - 2)$

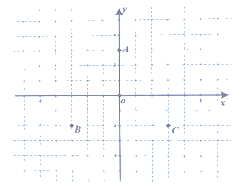(1)、图中点 $C$ 的坐标是；

(2)、三角形 $A B C$ 的面积为；

(3)、点 $C$ 关于 $x$ 轴对称的点 $D$ 的坐标是；

(4)、如果将点 $B$ 沿着 $x$ 轴平行的方向向右平移3个单位得到点 $B^{'}$ ，那么 $A$ 、 $B^{'}$ 两点之间的距离是；

(5)、图中四边形 $A B C D$ 的面积是.

查看试题解析
22. 小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校，以下是他本次上学所用的时间与路程的关系示意图，根据图中提供的信息回答下列问题：

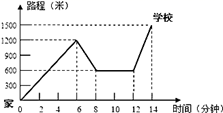(1)、小明家到学校的路程是米；

(2)、小明在书店停留了分钟；

(3)、本次上学途中，小明一共行驶了米，一共用了分钟；

(4)、在整个上学的途中(哪个时间段)小明骑车速度最快，最快的速度是米/分．

查看试题解析
23. 某校八年级的体育老师为了解本年级学生对球类运动的爱好情况，抽取了该年级部分学生对篮球、足球、排球、乒乓球的爱好情况进行了调查，并将调查结果绘制成图1和图2所示的两幅不完整的统计图（说明：每位学生只选一种自己最喜欢的一种球类）请根据这两幅图形解答下列问题：
　

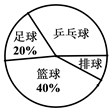
图 1 图 2

(1)、此次被调查的学生总人数为多少人？

(2)、分别求爱好篮球和排球的学生人数，并将条形统计图补充完整；

(3)、已知该校有 800 名学生，请你根据调查结果估计爱好篮球和排球的学生共有多少人？

查看试题解析
24. 学校准备租用甲乙两种大客车共1 辆，送师生集体外出参加活动，每辆甲种客车的租金是400元，每辆乙种客车的租金是250元，设租用甲种客车x辆，租车费用为y元．

(1)、求出y与x的函数关系式；

(2)、若租用甲种客车不少于6辆，应如何租用甲乙两种大客车，租车费用最低？最低费用是多少？

查看试题解析
25. 如图，直线 y＝kx+b 与 x 轴，y 轴分别交于点 A，点 B，点 A 的坐标为（﹣2，0），点 B 的坐标为 B（0，4）．

(1)、求直线 AB 解析式；

(2)、如图，将△AOB 向右平移 6 个单位长度，得到△A₁O₁B₁ ，求线段OB₁的长；

(3)、求（2）中△AOB 扫过的面积．

查看试题解析
26. 如图，△ABC 的中线 AD、BE、CF 相交于点 G，H、I 分别是 BG、CG 的中点．

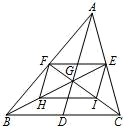(1)、是△ABC 的中位线，EF 与 BC 位置关系是、数量关系是；是△GBC 的中位线，HI 与 BC 位置关系是、数量关系是；

(2)、求证：四边形 EFHI 是平行四边形；

(3)、当 AD 与 BC 满足条件时，四边形 EFHI 是矩形；（直接写出结论）当 AD 与 BC 满足条件时，四边形 EFHI 是菱形．（直接写出结论）

查看试题解析