贵州省黔南州2020年中考数学试卷
试卷更新日期:2020-09-14 类型:中考真卷
一、选择题(本题10小题,每题4分,共40分)
-
1. 3的相反数是( )A、﹣3 B、3 C、﹣ D、2. 观察下列图形,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 某市2020年参加中考的考生人数的为93400人,将93400用科学记数法表示为( )A、934×102 B、93.4×103 C、9.34×104 D、0.934×1054. 下列四个几何体中,左视图为圆的是( )A、
3. 某市2020年参加中考的考生人数的为93400人,将93400用科学记数法表示为( )A、934×102 B、93.4×103 C、9.34×104 D、0.934×1054. 下列四个几何体中,左视图为圆的是( )A、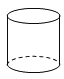 B、
B、 C、
C、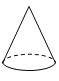 D、
D、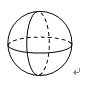 5. 下列运算正确的是( )A、(a3)4=a12 B、a3•a4=a12 C、a2+a2=a4 D、(ab)2=ab26. 如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=30°,则∠α的度数是( )
5. 下列运算正确的是( )A、(a3)4=a12 B、a3•a4=a12 C、a2+a2=a4 D、(ab)2=ab26. 如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=30°,则∠α的度数是( )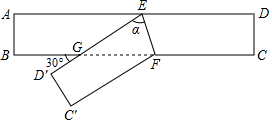 A、30° B、45° C、74° D、75°7. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
A、30° B、45° C、74° D、75°7. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )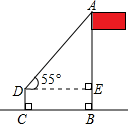 A、tan55°= B、tan55°= C、sin55°= D、cos55°=8. 某超市正在热销一种商品,其标价为每件12元,打8折销售后每件可获利2元,该商品每件的进价为( )A、7.4元 B、7.5元 C、7.6元 D、7.7元9. 已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( )A、9 B、17或22 C、17 D、2210. 已知a= ﹣1,a介于两个连续自然数之间,则下列结论正确的是( )A、1<a<2 B、2<a<3 C、3<a<4 D、4<a<5
A、tan55°= B、tan55°= C、sin55°= D、cos55°=8. 某超市正在热销一种商品,其标价为每件12元,打8折销售后每件可获利2元,该商品每件的进价为( )A、7.4元 B、7.5元 C、7.6元 D、7.7元9. 已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( )A、9 B、17或22 C、17 D、2210. 已知a= ﹣1,a介于两个连续自然数之间,则下列结论正确的是( )A、1<a<2 B、2<a<3 C、3<a<4 D、4<a<5二、填空题(本题10小题,每题3分,共30分)
-
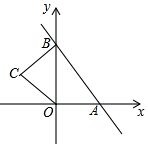
11. 分解因式:a3﹣2a2b+ab2= .12. 若单项式am﹣2bn+7与单项式﹣3a4b4的和仍是一个单项式,则m﹣n=.13. 若一组数据2,3,x,1,5,7的众数为7,则这组数据的中位数为.14. 函数y=x﹣1的图象一定不经过第象限.15. 如图,在平面直角坐标系中,直线y=﹣ x+4与x轴、y轴分别交于A、B两点,点C在第二象限,若BC=OC=OA,则点C的坐标为.
 16. 如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB= ,则AD长度是.
16. 如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB= ,则AD长度是.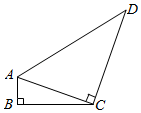 17. 已知菱形的周长为4 ,两条对角线长的和为6,则菱形的面积为.18. 如图,正方形ABCD的边长为10,点A的坐标为(﹣8,0),点B在y轴上,若反比例函数y= (k≠0)的图象过点C,则该反比例函数的解析式为.
17. 已知菱形的周长为4 ,两条对角线长的和为6,则菱形的面积为.18. 如图,正方形ABCD的边长为10,点A的坐标为(﹣8,0),点B在y轴上,若反比例函数y= (k≠0)的图象过点C,则该反比例函数的解析式为.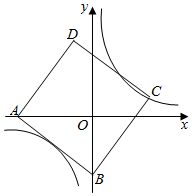 19. 《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
19. 《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为 .
20. 对于实数a,b,定义运算“*“,a*b= 例如4*2,因为4>2,所以4*2=42﹣4×2=8.若x1 , x2是一元二次方程x2﹣8x+16=0的两个根,则x1*x2=.三、解答题(本题6小题,共80分)
-
21.(1)、计算(﹣ )﹣1﹣3tan60°+|﹣ |+(2cos60°﹣2020)0;(2)、解不等式组 .22. 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的圆”,请研究如下美丽的圆,如图,Rt△ABC中,∠BCA=90°,AC=3,BC=4,点O在线段BC上,且OC= ,以O为圆心.OC为半径的⊙O交线段AO于点D,交线段AO的延长线于点E.
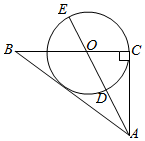 (1)、求证:AB是⊙O的切线;(2)、研究过短中,小明同学发现 = ,回答小明同学发现的结论是否正确?如果正确,给出证明;如果不正确,说明理由.23. 勤劳是中生民的传統美德,学校要求学们在家帮助父母做一些力所能及的家务.在学期初,小丽同学随机调查了七年级部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果绘制了如图两幅不完整的统计图:
(1)、求证:AB是⊙O的切线;(2)、研究过短中,小明同学发现 = ,回答小明同学发现的结论是否正确?如果正确,给出证明;如果不正确,说明理由.23. 勤劳是中生民的传統美德,学校要求学们在家帮助父母做一些力所能及的家务.在学期初,小丽同学随机调查了七年级部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果绘制了如图两幅不完整的统计图: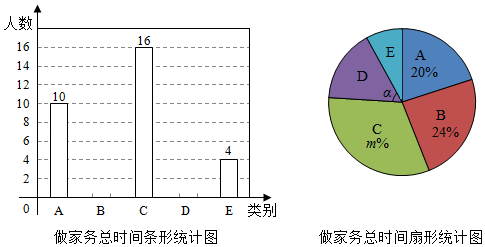
根据统计图提供的作息,解答下列问题:
(1)、本次共调查了名学生;(2)、根据以上信息直接在答题卡上补全条形统计图;(3)、扇形統计图中m= , 类别D所对应的扇形圆心角α的度数是度;(4)、若该校七年级共有400名学生,根据抽样调查的结果,估计该校七年級有多少名学生寒假在家做家务的总时间不低于20小时?24. 某单位计划购买甲、乙两种品牌的消毒剂,乙种品牌消毒剂每瓶的价格比甲种品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲种品牌消毒剂的数量与用400元购买乙种品牌消毒剂的数量相同.(1)、求甲、乙两种品牌消毒剂每瓶的价格各是多少元?(2)、若该单位从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙种品牌消毒剂?25. 在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全同学共通过多少次电话呢?我们可以用下面的方式来解决问题.用点A1、A2、A3…A48分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:
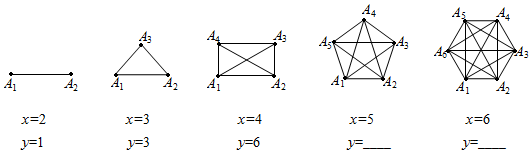 (1)、填写上图中第四个图中y的值为 , 第五个图中y的值为.(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当x=48时,对应的y=.(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?26. 如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF.
(1)、填写上图中第四个图中y的值为 , 第五个图中y的值为.(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当x=48时,对应的y=.(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?26. 如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF.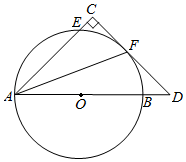 (1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.27. 如图(1),在平面直角坐标系中,抛物线y=ax2+bx+4(a≠0)与y轴交于点A,与x轴交于点C(﹣2,0),且经过点B(8,4),连接AB,BO,作AM⊥OB于点M,将Rt△OMA沿y轴翻折,点M的对应点为点N.解答下列问题:
(1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.27. 如图(1),在平面直角坐标系中,抛物线y=ax2+bx+4(a≠0)与y轴交于点A,与x轴交于点C(﹣2,0),且经过点B(8,4),连接AB,BO,作AM⊥OB于点M,将Rt△OMA沿y轴翻折,点M的对应点为点N.解答下列问题: (1)、抛物线的解析式为 , 顶点坐标为;(2)、判断点N是否在直线AC上,并说明理由;(3)、如图(2),将图(1)中Rt△OMA沿着OB平移后,得到Rt△DEF.若DE边在线段OB上,点F在抛物线上,连接AF,求四边形AMEF的面积.
(1)、抛物线的解析式为 , 顶点坐标为;(2)、判断点N是否在直线AC上,并说明理由;(3)、如图(2),将图(1)中Rt△OMA沿着OB平移后,得到Rt△DEF.若DE边在线段OB上,点F在抛物线上,连接AF,求四边形AMEF的面积.