山西省朔州市右玉县二中2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 要使式子 有意义,则 x 的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、4. 矩形,菱形,正方形都具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角5. 已知点(-2,y1),(1,0),(3,y2)都在一次函数y=kx-2的图象上,则y1 , y2 , 0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y16. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
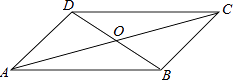 A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC7. 如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC7. 如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )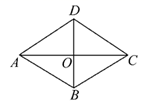 A、24 B、48 C、40 D、208. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
A、24 B、48 C、40 D、208. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、 B、
B、 C、
C、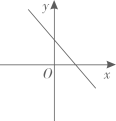 D、
D、 9. 如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为( )
9. 如图,四边形ABCD是菱形,对角线AC=8,DB=6,DH⊥AB于点H,则DH的长为( ) A、4.8cm B、5cm C、9.6cm D、10cm10. 如图,函数 和 的图象相交于A(m,3),则不等式 的解集为( )
A、4.8cm B、5cm C、9.6cm D、10cm10. 如图,函数 和 的图象相交于A(m,3),则不等式 的解集为( )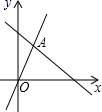 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若一个直角三角形的其中两条边长分别为6和8,则第三边长为.12. 已知菱形的两条对角线长分别为1和4,则菱形的面积为 .13. 将直线 向下平移1个单位长度后得到的图像的函数解析式是.14. 已知a、b、c是△ABC三边的长,且满足关系式 ,
则△ABC的形状为
15. 如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为 .
三、解答题
-
16. 计算(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)、(10)、(11)、(12)、17. 如图,已知在△ABC中,CD⊥AB于D , AC=20,BC=15,DB=9.求AB的长.
 18. 如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.
18. 如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.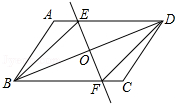 19. 如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,求证:AF⊥DE.
19. 如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,求证:AF⊥DE. 20. 小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
20. 小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.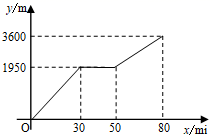 (1)、小亮行走的总路程是m,他途中休息了min.(2)、①当50≤x≤80时,求y与x的函数关系式;
(1)、小亮行走的总路程是m,他途中休息了min.(2)、①当50≤x≤80时,求y与x的函数关系式;②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?
21. 已知,直线y=2x+4与直线y=-2x-2. (1)、直接写出两直线与y轴交点A,B的坐标;(2)、求两直线交点C的坐标;(3)、求△ABC的面积.
(1)、直接写出两直线与y轴交点A,B的坐标;(2)、求两直线交点C的坐标;(3)、求△ABC的面积.

