重庆市西北狼教育联盟2020-2021学年八年级上学期数学开学试卷
试卷更新日期:2020-09-14 类型:开学考试
一、选择题:(本大题共12小题,每小题4分,共48分)
-
1. 计算 的结果是( )A、 B、 C、 D、32. 下列世界博览会会徽图案中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件中,必然事件是( )A、打开电视机,正在播“新冠肺炎”相关新闻 B、明天会下雨 C、小明今天至少走了 100 米 D、太阳从东方升起4. 下面四个图形中,∠1与∠2是对顶角的是( )
3. 下列事件中,必然事件是( )A、打开电视机,正在播“新冠肺炎”相关新闻 B、明天会下雨 C、小明今天至少走了 100 米 D、太阳从东方升起4. 下面四个图形中,∠1与∠2是对顶角的是( )
A、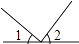 B、
B、 C、
C、 D、
D、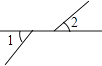 5. 下列各式计算正确的是( )A、 B、 C、 D、6. 一个盒子里装有红、黄、白球分别为 3、4、5个,这些球除颜色外都相同,从袋中任抽一个球,则抽到黄球的概率是( )A、 B、 C、 D、7. 如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )
5. 下列各式计算正确的是( )A、 B、 C、 D、6. 一个盒子里装有红、黄、白球分别为 3、4、5个,这些球除颜色外都相同,从袋中任抽一个球,则抽到黄球的概率是( )A、 B、 C、 D、7. 如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( )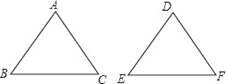 A、∠B=∠E,BC=EF B、∠A=∠D,BC=EF C、∠A=∠D,∠B=∠E D、BC=EF,AC=DF8. 如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=48°,则∠2的度数是( )
A、∠B=∠E,BC=EF B、∠A=∠D,BC=EF C、∠A=∠D,∠B=∠E D、BC=EF,AC=DF8. 如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=48°,则∠2的度数是( ) A、64° B、65° C、66° D、67°9. 将一副三角板按图中方式叠放,则角α等于( )
A、64° B、65° C、66° D、67°9. 将一副三角板按图中方式叠放,则角α等于( ) A、75° B、60° C、45° D、30°10. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作时间为t,剩下的水量为s,下面能反映s与t之间关系的大致图像是( )A、
A、75° B、60° C、45° D、30°10. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作时间为t,剩下的水量为s,下面能反映s与t之间关系的大致图像是( )A、 B、
B、 C、
C、 D、
D、 11. 若 ,则 的值是( )A、-16 B、16 C、-4 D、412. 如图,AD∥BC,BD为 的角平分线,DE、DF分别是 和 的角平分线,且 ,则以下 与 的关系正确的是( )
11. 若 ,则 的值是( )A、-16 B、16 C、-4 D、412. 如图,AD∥BC,BD为 的角平分线,DE、DF分别是 和 的角平分线,且 ,则以下 与 的关系正确的是( )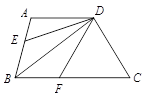 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:(本大题共6小题,每小题4分,共24分)
-
13. 2019新型冠状病毒(2019-nCoV),2020年1月12日被世界卫生组织命名.科学家借 助比光学显微镜更加厉害的电子显微镜发现新型冠状病毒的大小约为0.000000125 米.则数据0.000000125用科学记数法表示为.14. 已知: , 则 .15. 如图,直线 ,点 在直线 上,且 , = ,则 的度数是.
 16. 从长度分别为lcm、2cm、5cm、7cm、9cm的5根木棒中随机抽取一根,能与长度分别为3cm和5cm的木棒围成三角形的概率为.17. 某日小明步行,小颖骑车,他们同时从小颖家出发,以各自的速度匀速到公园去,小颖先到并停留了8分钟,发现相机忘在了家里,于是沿原路以同样的速度回家去取,已知小明的步行速度为180米/分钟,他们各自距离出发点的路程y与出发时间x之间的关系图象如图所示,则当小明到达公园的时候小颖离家米.
16. 从长度分别为lcm、2cm、5cm、7cm、9cm的5根木棒中随机抽取一根,能与长度分别为3cm和5cm的木棒围成三角形的概率为.17. 某日小明步行,小颖骑车,他们同时从小颖家出发,以各自的速度匀速到公园去,小颖先到并停留了8分钟,发现相机忘在了家里,于是沿原路以同样的速度回家去取,已知小明的步行速度为180米/分钟,他们各自距离出发点的路程y与出发时间x之间的关系图象如图所示,则当小明到达公园的时候小颖离家米. 18. 小林在测量如图所示的四边形ABCD时,测得该四边形的面积为32cm²,AB=AD,∠BAD=∠BCD=90°他马上得到AC的长度为 cm
18. 小林在测量如图所示的四边形ABCD时,测得该四边形的面积为32cm²,AB=AD,∠BAD=∠BCD=90°他马上得到AC的长度为 cm
三、解答题:(本大题共7小题,每小题10分,共70分)
-
19. 计算:(1)、 ;(2)、20. 完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.

求证:BE∥DF.
证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴+∠C=180°.
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1= ∠ABC.
同理,∠2= ∠ADC.
∴∠1=∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
21. 如图(1)、(2)所示,方格图中每个小正方形的边长为1,点A、B、C都是格点.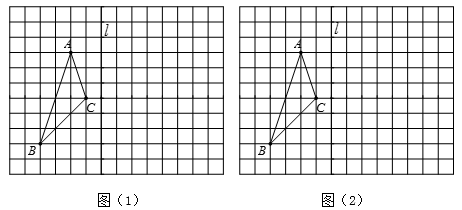 (1)、在(1)画中出△ABC关于直线l对称的 ;(2)、求出图(1)中 的面积;(3)、如图(2)所示,A、C是直线l同侧固定的点,P是直线l上的一个动点,在图(2)中的直线l上画出点P,使AP+PC的值最小.22. 先化简,再求值:
(1)、在(1)画中出△ABC关于直线l对称的 ;(2)、求出图(1)中 的面积;(3)、如图(2)所示,A、C是直线l同侧固定的点,P是直线l上的一个动点,在图(2)中的直线l上画出点P,使AP+PC的值最小.22. 先化简,再求值:,其中 , .
23. 一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题: (1)、农民自带的零钱是多少?(2)、降价前他每千克西瓜出售的价格是多少?(3)、随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?(4)、请问这个水果贩子一共赚了多少钱?24. 如图,在 中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得 ,连CF.
(1)、农民自带的零钱是多少?(2)、降价前他每千克西瓜出售的价格是多少?(3)、随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?(4)、请问这个水果贩子一共赚了多少钱?24. 如图,在 中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得 ,连CF. (1)、求证:(2)、若 ,连接BE,BE平分 ,AC平分 ,求 的度数.25. 定义:对于一个自然数,如果这个数除以5余数为4,且除以3余数为2,则称这个数为“差一数”.例如: , ,所以14是“差一数”; ,但 ,所以19不
(1)、求证:(2)、若 ,连接BE,BE平分 ,AC平分 ,求 的度数.25. 定义:对于一个自然数,如果这个数除以5余数为4,且除以3余数为2,则称这个数为“差一数”.例如: , ,所以14是“差一数”; ,但 ,所以19不 “差一数”. (1)、判断49和74是否为“差一数”?请说明理由;(2)、求大于300且小于400的所有“差一数”.
“差一数”. (1)、判断49和74是否为“差一数”?请说明理由;(2)、求大于300且小于400的所有“差一数”.四、解答题:(一个小题,共8分)
-
26. 某数学兴趣小组在一次探究活动中,把两个全等的直角三角形如图1放置,Rt△ABC≌Rt△DCB,∠ABC=∠DCB=90°,AC与BD相交于点O,发现OA=OB=OC=OD.把图1中的OD和CD擦除得到图2和结论:在Rt△ABC中,若OB是斜边AC上的中线,则有 .
 (1)、请在图1中证明OA=OB=OC=OD.(2)、如图3,在Rt△ABC中, ,∠C=26°,∠EFB的度数为:;(3)、如图4,在四边形ABCD中,BA⊥AC,BD⊥DC,点E是AD的中点,点F是BC的中点,猜想EF与AD的位置关系,并说明理由.
(1)、请在图1中证明OA=OB=OC=OD.(2)、如图3,在Rt△ABC中, ,∠C=26°,∠EFB的度数为:;(3)、如图4,在四边形ABCD中,BA⊥AC,BD⊥DC,点E是AD的中点,点F是BC的中点,猜想EF与AD的位置关系,并说明理由.