河北省沧州市河间市2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部分图形,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在式子 , , , , + ,9 x + ,中,分式的个数是( )A、5 B、4 C、3 D、23.
2. 在式子 , , , , + ,9 x + ,中,分式的个数是( )A、5 B、4 C、3 D、23.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
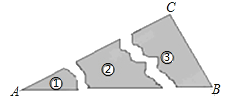 A、带①去 B、带②去 C、带③去 D、①②③都带去4. 下列计算正确的是( )A、a6÷a2=a4 B、(2a2)3=6a6 C、(a2)3=a5 D、(a+b)2=a2+b25. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )
A、带①去 B、带②去 C、带③去 D、①②③都带去4. 下列计算正确的是( )A、a6÷a2=a4 B、(2a2)3=6a6 C、(a2)3=a5 D、(a+b)2=a2+b25. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )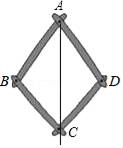 A、SSS B、SAS C、ASA D、AAS6. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形.根据图形的变化过程写出的一个正确的等式是( )
A、SSS B、SAS C、ASA D、AAS6. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形.根据图形的变化过程写出的一个正确的等式是( ) A、(a﹣b)2=a2﹣2ab+b2 B、a(a﹣b)=a2﹣ab C、(a﹣b)2=a2﹣b2 D、a2﹣b2=(a+b)(a﹣b)7. 若3x=4,3y=6,则3x-2y的值是( )A、 B、9 C、 D、38. 下列四个图形中,线段BE是△ABC的高的是( )A、
A、(a﹣b)2=a2﹣2ab+b2 B、a(a﹣b)=a2﹣ab C、(a﹣b)2=a2﹣b2 D、a2﹣b2=(a+b)(a﹣b)7. 若3x=4,3y=6,则3x-2y的值是( )A、 B、9 C、 D、38. 下列四个图形中,线段BE是△ABC的高的是( )A、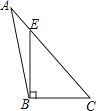 B、
B、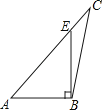 C、
C、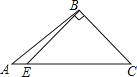 D、
D、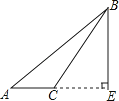 9. 小朱要到距家1500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱速度是x米/分,则根据题意所列方程正确的是( )A、 B、 C、 D、10. 已知实数x,y满足|x﹣4|+(y﹣8)2=0,则以x,y的值为两边长的等腰三角形的周长是( )A、20或16 B、20 C、16 D、以上答案均不对
9. 小朱要到距家1500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱速度是x米/分,则根据题意所列方程正确的是( )A、 B、 C、 D、10. 已知实数x,y满足|x﹣4|+(y﹣8)2=0,则以x,y的值为两边长的等腰三角形的周长是( )A、20或16 B、20 C、16 D、以上答案均不对二、填空题
-
11. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .12. 把多项式ax2+2axy+ay2分解因式的结果是 .
13. 当x=时,分式 的值为014. 如图所示:已知点F、E分别在AB、AC上,且AE=AF,请你补充一个条件: , 使得△ABE≌△ACF.(只需填写一种情况即可) 15. 如图所示,在 中, , ,AB的垂直平分线交AB于点D , 交AC于点E , 连接BE , 则 的度数为
15. 如图所示,在 中, , ,AB的垂直平分线交AB于点D , 交AC于点E , 连接BE , 则 的度数为 16. 阅读下面的材料,并解答问题:
16. 阅读下面的材料,并解答问题:分式 ( )的最大值是多少?
解: ,
因为x≥0,所以x+2的最小值是2,所以 的最大值是 ,所以 的最大值是4,即 (x≥0)的最大值是4.
根据上述方法,试求分式 的最大值是.
三、解答题
-
17. 先化简,再求值:(2x﹣3y)2+(x+3y)(x﹣3y),其中x=2,y=5.18. 如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
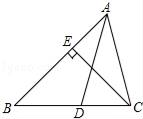 19. 阅读下列材料:
19. 阅读下列材料:小铭和小雨在学习过程中有如下一段对话:
小铭:“我知道一般当m≠n时,m2+n≠m+n2 . 可是我见到有这样一个神奇的等式: = +( )2(其中a,b为任意实数,且b≠0).你相信它成立吗?”
小雨:“我可以先给a,b取几组特殊值验证一下看看.”
完成下列任务:
(1)、请选择两组你喜欢的、合适的a,b的值,分别代入阅读材料中的等式,写出代入后得到的具体等式并验证它们是否成立;①当a= , b=时,等式(填写“成立”或“不成立”);
②当a= , b=时,等式(填写“成立”或“不成立”).
(2)、对于任意实数a,b(b≠0),通过计算说明 是否成立.20. 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58° (1)、求出BF的长度;(2)、求∠CAD的度数;21. 因雾霾天引发的汽车尾气污染备受关注,由此汽车限号行驶也成为人们关注的焦点,限行期间为方便市民出行,某路公交车每天比原来的运行增加15车次.经调研得知,原来这路公交车平均每天共运送乘客5600人,限行期间这路公交车平均每天共运送乘客8000人,且平均每车次运送乘客与原来的数量基本相同,问限行期间这路公交车每天运行多少车次?22. 如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠B有怎样的数量关系?
(1)、求出BF的长度;(2)、求∠CAD的度数;21. 因雾霾天引发的汽车尾气污染备受关注,由此汽车限号行驶也成为人们关注的焦点,限行期间为方便市民出行,某路公交车每天比原来的运行增加15车次.经调研得知,原来这路公交车平均每天共运送乘客5600人,限行期间这路公交车平均每天共运送乘客8000人,且平均每车次运送乘客与原来的数量基本相同,问限行期间这路公交车每天运行多少车次?22. 如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠B有怎样的数量关系?小明通过观察分析,形成了如下解题思路:如图2,延长AC到E,使CE=CD,连接DE.进而得到△ABD≌△AED,便可得到∠ACB与∠B的数量关系.请结合小明的思路,写出两个角的数量关系,并证明结论.
 23. 常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如 ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为: ,这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.(1)、分解因式: ;(2)、△ABC三边a、b、c满足 ,判断△ABC的形状.24. 在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)
23. 常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如 ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为: ,这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.(1)、分解因式: ;(2)、△ABC三边a、b、c满足 ,判断△ABC的形状.24. 在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)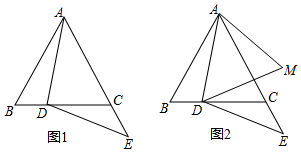 (1)、求证:∠BAD=∠EDC;(2)、如图2,点E关于直线BC的对称点为M,连接DM,AM.
(1)、求证:∠BAD=∠EDC;(2)、如图2,点E关于直线BC的对称点为M,连接DM,AM.小明通过观察,实验提出猜想:在点D运动的过程中,始终有DA=AM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的两种想法:
想法1:要证明DA=AM,只需证△ADM是等边三角形;
想法2:连接CM,只需证明△ABD≌△ACM即可.
请你参考上面的想法,帮助小明证明DA=AM(选一种方法即可)