河北省保定市定兴县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-14 类型:期末考试
一、单选题
-
1. 在平面直角坐标系 中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图,矩形 的两条对角线相交于点 , ,则线段 的长为( )
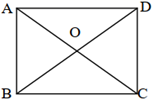 A、8 B、4 C、3 D、23. 为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,则仰卧起坐次数在25次(含25次)以上的人数共有( )
A、8 B、4 C、3 D、23. 为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,则仰卧起坐次数在25次(含25次)以上的人数共有( )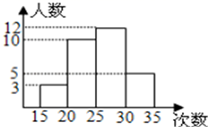 A、10人 B、12人 C、17人 D、都不对4. 已知一次函数 和一次函数 的图象的交点坐标是 ,据此可知方程组 的解为( )A、 B、 C、 D、5. 如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )
A、10人 B、12人 C、17人 D、都不对4. 已知一次函数 和一次函数 的图象的交点坐标是 ,据此可知方程组 的解为( )A、 B、 C、 D、5. 如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )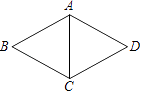 A、20 B、15 C、10 D、56. 如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A、20 B、15 C、10 D、56. 如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )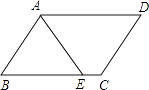 A、1 B、2 C、3 D、47. 如图,平移折线AEB , 得到折线CFD , 则平移过程中扫过的面积是( )
A、1 B、2 C、3 D、47. 如图,平移折线AEB , 得到折线CFD , 则平移过程中扫过的面积是( )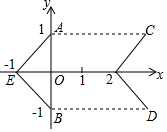 A、4 B、5 C、6 D、78. 如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则 为
A、4 B、5 C、6 D、78. 如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则 为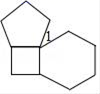 A、32° B、36° C、40° D、42°9.
A、32° B、36° C、40° D、42°9.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
 A、平行四边形 B、矩形 C、菱形 D、正方形10. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为( )
A、平行四边形 B、矩形 C、菱形 D、正方形10. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为( ) A、1 B、2 C、3 D、511. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、
A、1 B、2 C、3 D、511. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、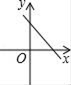 B、
B、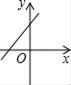 C、
C、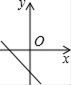 D、
D、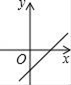 12. 已知点(-2,y1),(1,0),(3,y2)都在一次函数y=kx-2的图象上,则y1 , y2 , 0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y113. 如图,把一张正方形纸对折两次后,沿虚线剪下一角,展开后所得图形一定是( )
12. 已知点(-2,y1),(1,0),(3,y2)都在一次函数y=kx-2的图象上,则y1 , y2 , 0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y113. 如图,把一张正方形纸对折两次后,沿虚线剪下一角,展开后所得图形一定是( ) A、三角形 B、菱形 C、矩形 D、正方形14. 在一次活动课,数学老师要求同学们尺规作图:经过直线外一点作这条直线的平行线.题目出示如下:
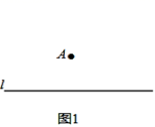
A、三角形 B、菱形 C、矩形 D、正方形14. 在一次活动课,数学老师要求同学们尺规作图:经过直线外一点作这条直线的平行线.题目出示如下:已知:如图1直线 和直线 外一点 .求作:直线 的平行线,使它经过点 .
小亮的作法如下:
如图2,(1)过点 作直线 交直线 于点 ;(2)以点 为圆心, 长为半径作弧,交直线 于点 ;(3)在直线 上取点 (不与点 重合),连接 ;(4)作线段 的垂直平分线 ,交线段 于点 ;(5)作直线 .所以直线 即为所求.
老师表扬了小亮的作法是对的.
请你回答:小亮这样作图的主要依据是( )
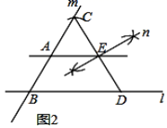 A、三角形的中位线平行于第三边 B、线段垂直平分线的性质定理 C、平行公理 D、以上答案都不对15. 如表是变量 与 之间的一组数据,则 与 之间的表达式可以写成( )
A、三角形的中位线平行于第三边 B、线段垂直平分线的性质定理 C、平行公理 D、以上答案都不对15. 如表是变量 与 之间的一组数据,则 与 之间的表达式可以写成( )1
2
3
4
……
2
5
10
17
……
A、 B、 C、 D、16. 如图1,在矩形ABCD中,AB=2,动点P从点B出发,沿路线B→C→D作匀速运动,图2是此运动过程中,△PAB的面积S与点P运动的路程x之间的函数图象的一部分,则BC+CD的长为( )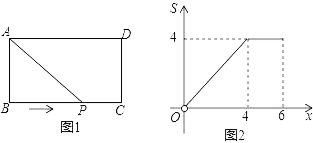 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
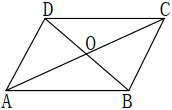
17. 函数y= 中自变量x的取值范围是 .18. 如图所示,平行四边形 的周长为60厘米,对角线相交于点 , 的周长比 的周长小8厘米,则 , 的长分别为厘米、厘米.
 19.
19.用黑白两种颜色的正六边形地面砖按如图所示的规律,拼成若干图案:
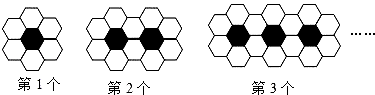 (1)、第4个图案有白色地面砖块;(2)、第n个图案有白色地面砖块.
(1)、第4个图案有白色地面砖块;(2)、第n个图案有白色地面砖块.三、解答题
-
20. 在平面直角坐标系中,已知点 ,请解答下列问题:(1)、若点 在第三象限,则 的取值范围为(2)、若点 在 轴上,则 的值为(3)、当 时,点 关于 轴对称的点的坐标为点 关于原点对称的点的坐标为21. 某剧院的观众席的座位为扇形,且按下列方式设置:
排数( )
1
2
3
4
……
座位数( )
50
53
56
59
……
(1)、按照上表所示的规律,当 每增加1时, 如何变化?.(2)、写出座位数 与排数 之间的解析式.(3)、按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.22. 某校为了解八年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位: )分成五组( :39.5~46.5; :46.5~53.5; :53.5~60.5; :60.5~67.5; :67.5~74.5),并依据统计数据绘制了如下两种尚不完整的统计图.解答下列问题:
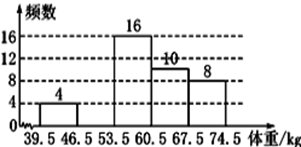
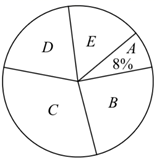 (1)、这次抽样调查的样本容量是 , 并补全频数分布直方图;(2)、 组学生的频率为 , 在扇形统计图中 组的圆心角是度;(3)、请你估计该校九年级体重超过 的学生大约有多少名.23. 已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数 的图象相交于点(2,a).
(1)、这次抽样调查的样本容量是 , 并补全频数分布直方图;(2)、 组学生的频率为 , 在扇形统计图中 组的圆心角是度;(3)、请你估计该校九年级体重超过 的学生大约有多少名.23. 已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数 的图象相交于点(2,a).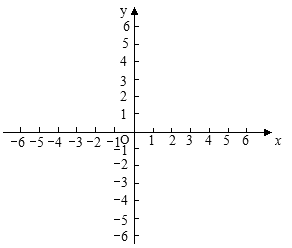 (1)、求a的值.(2)、求一次函数y=kx+b的表达式.
(1)、求a的值.(2)、求一次函数y=kx+b的表达式.
(3)、在同一坐标系中,画出这两个函数的图象.24. 老师布置了一个作业,如下:已知:如图1 的对角线 的垂直平分线 交 于点 ,交 于点 ,交 于点 .求证:四边形 是菱形.
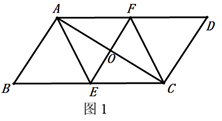

嘉琪同学写出了如图2所示的证明过程,老师说嘉琪同学的作业是错误的.请你解答下列问题:
(1)、能找出该同学错误的原因吗?请你指出来;(2)、请你给出本题的符合题意证明过程.25. 已知:如图,在菱形 中,点 , , 分别为 , , 的中点,连接 , , , .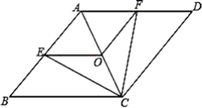 (1)、求证: ;(2)、当 与 满足什么关系时,四边形 是正方形?请说明理由.26. 某大型水果批发市场,对购买量在1900斤至6000斤之间(含1900斤和6000斤)的批发商,市场有两种销售方案(批发商只能选择其中一种方案购买):
(1)、求证: ;(2)、当 与 满足什么关系时,四边形 是正方形?请说明理由.26. 某大型水果批发市场,对购买量在1900斤至6000斤之间(含1900斤和6000斤)的批发商,市场有两种销售方案(批发商只能选择其中一种方案购买):方案 :每斤4.5元,由批发市场免费送货.
方案 :每斤4元,批发商需先支付运费1200元,再由批发市场送货.
(1)、请分别写出按方案 、方案 购买水果的应付款 (元)与购买量 (斤)之间的函数解析式.(2)、当 时,批发商选择哪种方案付款比较划算?(3)、某批发商计划用10350元尽可能多购买这家市场的水果,他应选择哪种方案?