广东省中山市2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式，是最简二次根式的是（）

A、 $\sqrt{1}$ B、 $\sqrt{4}$ C、 $\sqrt{8}$ D、 $\sqrt{3}$

查看试题解析
2. 某市五月份连续五天的日最高气温分别为33、30、31、31、29（单位：℃），这组数据的众数是（）

A、29 B、30 C、31 D、33

查看试题解析
3. 下列各组数，不能作为直角三角形的三边长的是（）

A、3，4，5 B、1，1， $\sqrt{2}$ C、2，3，4 D、6，8，10

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{8} = 4$ C、 ${(\sqrt{3})}^{2} = 6$ D、 $\sqrt{10} \div 2 = \sqrt{5}$

查看试题解析
5. 甲、乙、丙三个旅行团的游客人数都相等，且每个团游客的平均年龄都是35岁，这三个团游客年龄的方差分别是 $S_{甲}^{2} =$ 28， $S_{乙}^{2} =$ 18.6， $S_{丙}^{2} =$ 1.7．导游小李最喜欢带游客年龄相近的团队，若在三个团中选择一个，则他应选（）

A、甲团 B、乙团 C、丙团 D、三个团都一样

查看试题解析
6. 如图，□ABCD的对角线相交于点O ，下列式子不一定正确的是（）

A、AC＝BD B、AB＝CD C、∠BAD＝∠BCD D、AO＝CO

查看试题解析
7. 如图，矩形ABCD中，∠AOB＝60°，AB＝3，则BD的长是（）

A、3 B、5 C、 $3 \sqrt{3}$ D、6

查看试题解析
8. 已知关于x的一次函数y＝kx＋2k－3的图象经过原点，则k的值为（）

A、0 B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、3

查看试题解析
9. 对于函数y＝- $\frac{1}{2}$ x＋1，下列结论正确的是（）

A、它的图象不经过第四象限 B、y的值随x的增大而增大 C、它的图象必经过点（0，1） D、当x＞2时，y＞0

查看试题解析
10. 下列命题的逆命题成立的是（）

A、对顶角相等 B、两直线平行，同位角相等 C、如果a＝b ，那么a²＝b² D、正方形的四条边相等

查看试题解析

二、填空题

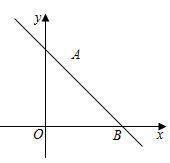
11. 某车间5名工人日加工零件数依次为6、9、5、5、4，则这组数据的中位数是．

查看试题解析
12. 若二次根式 $\sqrt{3 + x}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
13. 在▱ABCD中，∠A＝105º，则∠D＝．

查看试题解析
14. 正方形的边长为 $\sqrt{2}$ ，则这个正方形的对角线长为．

查看试题解析
15. 如图，直线y＝kx＋3经过点A（1，2），则它与x轴的交点B的坐标为．

查看试题解析
16. 如图，在菱形ABCD中，∠C＝60º，E、F分别是AB、AD的中点，若EF＝5，则菱形ABCD的周长为．

查看试题解析
17. 如图，在平面直角坐标系中，直线y＝ $\frac{4}{5}$ x－1与矩形OABC的边BC、OC分别交于点E、F ，已知OA＝3，OC＝4，则 $△ C E F$ 的面积是．

查看试题解析

三、解答题

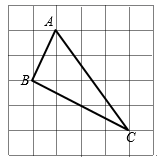
18. 计算： $(3 \sqrt{2} - \sqrt{6})$ ÷ $\sqrt{2} + \sqrt{3} (1 - \sqrt{12})$

查看试题解析
19. 学校规定学生的学期总评成绩满分为100分，学生的学期总评成绩根据平时成绩、期中考试成绩和期末考试成绩按照2∶3∶5的比确定，小欣的数学三项成绩依次是85、90、94，求小欣这学期的数学总评成绩．

查看试题解析
20. 如图，每个小正方形的边长均为1，求证：△ABC是直角三角形．

查看试题解析
21. 某中学为了了解学生对四大古典名著的阅读情况，就“四大古典名著你读完了几部”的问题对全校学生进行了抽样调查，根据调查结果绘制成如图所示的两个不完整的统计图，请结合图中信息解决下列问题：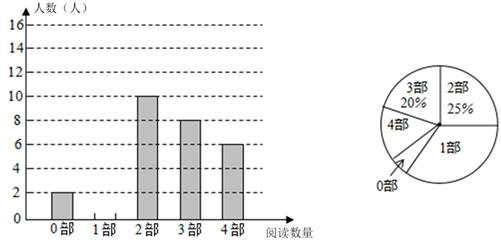

(1)、请将条形统计图补充完整，本次调查所得数据的众数是，中位数是；

(2)、请通过计算估计全校学生平均每人大约阅读多少部四大古典名著．

查看试题解析
22. 某通讯公司推出①、②两种收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间的函数关系如图所示．

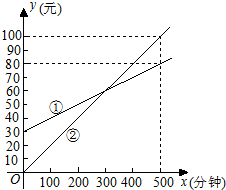(1)、分别求出①、②两种收费方式中y与自变量x之间的函数关系式；

(2)、何时两种收费方式费用相等？

查看试题解析
23. 如图，▱ABCD的对角线AC、BD相交于点O ， AC平分∠BAD ， DP//AC ， CP//BD ．

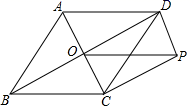(1)、求证：四边形ABCD是菱形；

(2)、若AC＝4，BD＝6，求OP的长．

查看试题解析
24. 如图，正方形ABCD中，点E是边BC上一点，EF⊥AC于点F ，点P是AE的中点．

(1)、求证：BP⊥FP；

(2)、连接DF ，求证：AE＝ $\sqrt{2}$ DF ．

查看试题解析
25. 如图，直线y＝ $\frac{3}{4}$ x＋9分别交x轴、y轴于点A、B ， ∠ABO的平分线交x轴于点C ．

(1)、求点A、B、C的坐标；

(2)、若点M与点A、B、C是平行四边形的四个顶点，求CM所在直线的解析式．

查看试题解析