广东省广州市番禺区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x - 2}$ 有意义，x必须满足（）

A、x≤2 B、x≥2 C、x＜2 D、x＞2

查看试题解析
2. 下列各组数中不能作为直角三角形的三边长的是（）

A、3，4，5 B、13，14，15 C、5，12，13 D、15，8，17

查看试题解析
3. 下面是某八年级（2）班第1组女生的体重（单位：kg）：35，36，42，42，68，40，38，这7个数据的中位数是（）

A、68 B、43 C、42 D、40

查看试题解析
4. 矩形，菱形，正方形都具有的性质是（）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角

查看试题解析
5. 一次函数 $y = - 3 x + 1$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，在菱形ABCD中，E ， F分别是AB ， AC的中点，若EF=2，则菱形ABCD的周长为（）

A、16 B、8 C、 $4 \sqrt{2}$ D、4

查看试题解析
7. 下列各式计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\frac{\sqrt{18} - \sqrt{8}}{\sqrt{2}} = \sqrt{9} - \sqrt{4} = 3 - 2 = 1$

查看试题解析
8. 把直线y＝﹣2x向上平移后得到直线AB ，若直线AB经过点（m ， n），且2m+n＝8，则直线AB的表达式为（）

A、y＝﹣2x+4 B、y＝﹣2x+8 C、y＝﹣2x﹣4 D、y＝﹣2x﹣8

查看试题解析
9. 如图，以正方形ABCD的边AD为一边作等边△ADE，则∠AEB等于（）

A、10° B、15° C、20° D、12.5°

查看试题解析
10. 如图，在菱形ABCD中，AB=AC=1，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，连接DH交AC于点O，则下列结论：①△ABF≌△CAE；②∠FHC=∠B；③△ADO≌△ACH；④ $S_{菱形 A B C D} = \sqrt{3}$ ；其中正确的结论个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： $\sqrt{3}$ × $\sqrt{5}$ ＝.

查看试题解析
12. 在 $▱ A B C D$ 中，若∠A=38°，则∠C=

查看试题解析
13. 直线 $y = 2 x - 3$ 与 $y$ 轴的交点坐标

查看试题解析
14. 两人从同一地点同时出发，一人以30m/min的速度向北直行，一人以30m/min的速度向东直行，10min后他们相距m

查看试题解析
15. 甲、乙两车从A城出发前往B城．在整个行程中，汽车离开A城的距离 $y$ 与时刻 $t$ 的对应关系如图所示，则当乙车到达B城时，甲车离B城的距离为km．

查看试题解析
16. 如图，在矩形ABCD中，AB=6，BC=4，将矩形沿AC折叠，点D落在 $D^{'}$ 处，则重叠部分△AFC的面积为

查看试题解析

三、解答题

17. 计算：

(1)、 $5 \sqrt{2} - 2 \sqrt{2}$

(2)、 $(2 \sqrt{3} + \sqrt{6}) (2 \sqrt{3} - \sqrt{6})$

(3)、 $\frac{2}{3} \sqrt{9 x} + 6 \sqrt{\frac{x}{4}}$

查看试题解析
18. 甲、乙两名射击运动员各进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9．乙的成绩如图所示（单位：环）

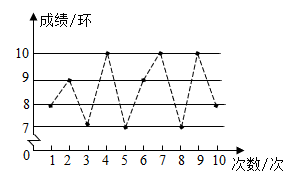(1)、分别计算甲、乙两人射击成绩的平均数；

(2)、若要选拔一人参加比赛，应派哪一位？请说明理由．

查看试题解析
19. 如图，一架2.5m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4m，如果梯子的顶端A沿墙下滑0.4m，则梯子底端B也外移0.4m吗？为什么？

查看试题解析
20. 已知直线 $y = k x + b$ 的图象经过点 $(2, 4)$ 和点 $(- 2, - 2)$

(1)、求 $b$ 的值；

(2)、求关于 $x$ 的方程 $k x + b = 0$ 的解

(3)、若 $(x_{1}, y_{1})$ 、 $(x_{2}, y_{2})$ 为直线上两点，且 $x_{1} < x_{2}$ ，试比较 $y_{1}$ 、 $y_{2}$ 的大小

查看试题解析
21. 如图，在 $▱ A B C D$ 中，BE∥DF，且分别交对角线AC于点E，F，连接ED，BF．

(1)、求证：AE=CF

(2)、若AB=9，AC=16，AE=4，BF= $3 \sqrt{7}$ ，求四边形ABCD的面积．

查看试题解析
22. 已知点A $(8 ， 0)$ 及第一象限的动点 $P (x ， y)$ ，且 $x + y = 10$ ，设△OPA的面积为S．

(1)、求S关于x的函数解析式，并写出x的取值范围；

(2)、画出函数S的图象，并求其与正比例函数 $S = 2 x$ 的图象的交点坐标；

(3)、当S=12时，求P点坐标．

查看试题解析
23. 如图，在平行四边形ABCD中，E，F分别是AB，CD的中点，DE，BF与对角线AC分别交于点M，N，连接MF，NE．

(1)、求证：DE∥BF

(2)、判断四边形MENF是何特殊的四边形？并对结论给予证明；

查看试题解析
24. 甲、乙两家商场平时以同样价格出售相同的商品，春节期间两家商场都让利酬宾，其中甲商场所有商品按8折出售，乙商场对一次购物中超过300元后的价格部分打7折．

(1)、以 $x$ （单位：元）表示商品原价， $y$ （单位：元）表示购物金额，分别就两家商场的让利方式写出 $y$ 与 $x$ 的函数解析式；

(2)、在同一直角坐标系中画出（1）中函数的图象；

(3)、春节期间如何选择这两家商场去购物更省钱？

查看试题解析
25. 如图，在边长为 $a$ 的正方形ABCD中，作∠ACD的平分线交AD于F ，过F作直线AC的垂线交AC于P ，交CD的延长线于Q ，又过P作AD的平行线与直线CF交于点E ，连接DE ， AE ， PD ， PB ．

(1)、求AC ， DQ的长；

(2)、四边形DFPE是菱形吗？为什么？

(3)、探究线段DQ ， DP ， EF之间的数量关系，并证明探究结论；

(4)、探究线段PB与AE之间的数量关系与位置关系，并证明探究结论．

查看试题解析