广东省佛山市南海区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子是分式的是（）

A、 $\frac{3 x}{2}$ B、 $\frac{20}{x + y}$ C、x²y D、 $\frac{1}{π}$

查看试题解析
2. 将点P（2，1）沿x轴方向向左平移3个单位，再沿y轴方向向上平移2个单位，所得的点的坐标是（）

A、（1，1） B、（-1，3） C、（5，1） D、（5，3）

查看试题解析
3. 下列多项式中，不能因式分解的是（）

A、 $a b - a$ B、 $a^{2} - 9$ C、 $a^{2} + 2 a + 5$ D、 $4 a^{2} + 4 a + 1$

查看试题解析
4. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 小玲的爸爸在钉制平行四边形框架时，采用了一种方法：如图所示，将两根木条AC、BD的中点重叠并用钉子固定，则四边形ABCD就是平行四边形，这种方法的依据是（）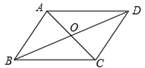

A、对角线互相平分的四边形是平行四边形 B、一组对边平行且相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、两组对边分别平行的四边形是平行四边形

查看试题解析
6. 如图，射线OC是∠AOB的角平分线，D是射线OC上一点，DP⊥OA于点P ， DP＝4，若点Q是射线OB上一点，OQ＝3，则△ODQ的面积是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 如果把分式 $\frac{3 x}{x - 2 y}$ 中的x、y的值都扩大为原来的3倍，那么分式的值（）

A、不变 B、扩大为原来的3倍 C、扩大为原来的6倍 D、扩大为原来的9倍

查看试题解析
8. 如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（）

A、点M B、格点N C、格点P D、格点Q

查看试题解析
9. 如图，在△ABC中，AB=AC，点D，E在BC上，连接AD，AE，如果只添加一个条件使∠DAB=∠EAC，则添加的条件不能为（）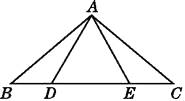

A、BD=CE B、AD=AE C、DA=DE D、BE=CD

查看试题解析
10. 如图，在△ABC中，AB＝3，AC＝4，BC＝5，△ABD ， △ACE ， △BCF都是等边三角形，下列结论中：①AB⊥AC；②四边形AEFD是平行四边形；③∠DFE＝150°；④S_四边形_AEFD＝5．正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. “m²是非负数”，用不等式表示为．

查看试题解析
12. 已知分式 $\frac{x + 2}{x^{2} - 4 x + a}$ ，当x＝1时，分式无意义，则a＝．

查看试题解析
13. 已知 $x + y = 2019$ ， $x - y = \frac{2020}{2019}$ ，则 $x^{2} - y^{2}$ 的值为．

查看试题解析
14. 已知函数y₁=k₁x+b₁与函数y₂=k₂x+b₂的图象如图所示，则不等式k₁x+b₁＜k₂x+b₂的解集是．

查看试题解析
15. 如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AB＝10，将△ABC沿CB方向向右平移得到△DEF ．若四边形ABED的面积为20，则平移距离为．

查看试题解析
16. 如图，以正方形ABCD的BC边向外作正六边形BEFGHC ，则∠ABE＝度．

查看试题解析
17. 如图，小芳作出了边长为1的第1个正△A₁B₁C₁ ．然后分别取△A₁B₁C₁的三边中点A₂、B₂、C₂ ，作出了第2个正△A₂B₂C₂；用同样的方法，作出了第3个正△A₃B₃C₃ ， ……，由此可得，第 $n$ 个正△A_nB_nC_n的边长是．

查看试题解析

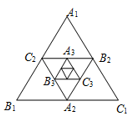
三、解答题

18. 解不等式组： ${\begin{array}{l} x + 2 > 0 ① \\ 2 (x - 1) + 3 \geq 3 x ② \end{array}$ ．

查看试题解析
19. 先化简，再求值： $\frac{x^{2} - 4}{x^{2} + 2 x} \div (x - \frac{4 x - 4}{x})$ ，其中x= $\sqrt{5}$ ．

查看试题解析
20. 如图，在□ABCD中，∠B＝60°．

(1)、作∠A的角平分线与边BC交于点E（用尺规作图，保留作图痕迹，不要求写作法）；

(2)、求证：△ABE是等边三角形．

查看试题解析
21. 本学期开学后，某校为了宣传关于新冠肺炎的防控知识，需印制若干份资料，印刷厂有甲、乙两种收费方式，甲种方式每份资料收费0.1元，另需收取制版费20元；乙种方式每份资料收费0.15元，不需要收取制版费．

(1)、设资料印刷的费用为y元，印刷的数量为x份，请分别写出两种收费方式下y与x之间的函数关系式；

(2)、该校某年级每次需印制100～600（含100和600）份资料，选择哪种印刷方式较合算？

查看试题解析
22. 如图，D是△ABC内一点，连接DB、DC、DA ，并将AB、DB、DC、AC的中点E、H、G、F依次连接，得到四边形EHGF ．

(1)、求证：四边形EHGF是平行四边形；

(2)、若BD⊥CD ， AD＝7，BD＝8，CD＝6，求四边形EHGF的周长．

查看试题解析
23. 李大伯响应国家保就业保民生政策合法摆摊，他预测某品牌新开发的小玩具能够畅销，就用3000元购进了一批小玩具，上市后很快脱销，他又用8000元购进第二批小玩具，所购数量是第一批购进数量的2倍，但每个进价贵了5元．

(1)、求李大伯第一次购进的小玩具有多少个？

(2)、如果这两批小玩具的售价相同，且全部售完后总利润率不低于20%，那么每个小玩具售价至少是多少元？

查看试题解析
24.

(1)、如图甲，从边长为a的正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形，然后拼成一个平行四边形（如图乙），那么通过计算两个图形阴影部分的面积，可以验证因式分解公式成立的是；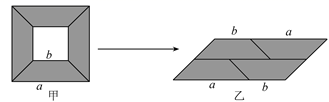

(2)、根据下面四个算式：
5²3²＝（5+3）×（53）＝8×2；

11²5²＝（11+5）×（115）＝16×6＝8×12；

15²3²＝（15+3）×（153）＝18×12＝8×27；

19²7²＝（19+7）×（197）＝26×12＝8×39．

请你再写出两个（不同于上面算式）具有上述规律的算式；

(3)、用文字写出反映（2）中算式的规律，并证明这个规律的符合题意性．

查看试题解析
25. 如图，在△ABC中，∠ACB＝90°，BC＝AC＝6，D是AB边上任意一点，连接CD ，以CD为直角边向右作等腰直角△CDE ，其中∠DCE＝90°，CD＝CE ，连接BE ．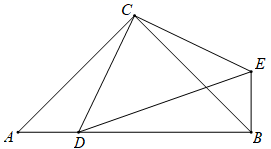

(1)、求证：AD＝BE；

(2)、当△CDE的周长最小时，求CD的值；

(3)、求证： $A D^{2} + D B^{2} = 2 C E^{2}$ ．

查看试题解析